The world of mathematics is filled with fascinating concepts, and one of the most intriguing is the parabola. A parabola is a U-shaped curve that is crucial in various branches of mathematics and science. Converting a parabola to its vertex form is an essential skill, and that's where the parabola to vertex form calculator tool comes into play. In this article, we'll delve into the world of parabolas, explore the concept of vertex form, and discuss how a calculator tool can simplify the process.
Understanding Parabolas

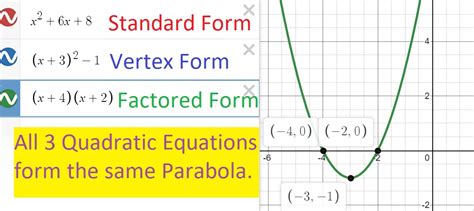
A parabola is a quadratic curve that is defined by the equation y = ax^2 + bx + c, where a, b, and c are constants. The parabola opens upward if a > 0 and downward if a < 0. The vertex of the parabola is the lowest or highest point on the curve, depending on the direction of the opening.
What is Vertex Form?
Vertex form is a way of expressing a parabola in terms of its vertex. The vertex form of a parabola is given by the equation y = a(x-h)^2 + k, where (h, k) is the vertex of the parabola. This form is useful for identifying the vertex and axis of symmetry of the parabola.
Converting a Parabola to Vertex Form

Converting a parabola to its vertex form involves completing the square. The process involves rewriting the quadratic equation in a form that allows us to easily identify the vertex. Here are the steps:
- Start with the standard form of the quadratic equation: y = ax^2 + bx + c
- Factor out the coefficient of x^2: y = a(x^2 + bx/a)
- Add and subtract (b/2a)^2 inside the parentheses: y = a(x^2 + bx/a + (b/2a)^2 - (b/2a)^2)
- Simplify the expression: y = a(x + b/2a)^2 - (b^2/4a) + c
- Write the equation in vertex form: y = a(x-h)^2 + k
How to Use a Parabola to Vertex Form Calculator Tool
A parabola to vertex form calculator tool can simplify the process of converting a parabola to its vertex form. Here's how to use it:
- Enter the coefficients a, b, and c of the quadratic equation
- Click the "Convert to Vertex Form" button
- The tool will display the vertex form of the parabola, including the coordinates of the vertex
Benefits of Using a Parabola to Vertex Form Calculator Tool

Using a parabola to vertex form calculator tool offers several benefits, including:
- Saves time: The tool can convert a parabola to its vertex form in seconds, saving you time and effort.
- Reduces errors: The tool eliminates the risk of human error, ensuring that the conversion is accurate.
- Improves understanding: The tool can help you understand the concept of vertex form and how to convert a parabola to its vertex form.
Real-World Applications of Parabolas
Parabolas have numerous real-world applications, including:
- Physics: Parabolas are used to describe the trajectory of projectiles, such as the path of a thrown ball.
- Engineering: Parabolas are used in the design of suspension bridges, antennas, and satellite dishes.
- Architecture: Parabolas are used in the design of buildings, such as the curved shape of a dome.
Conclusion
Converting a parabola to its vertex form is an essential skill in mathematics. A parabola to vertex form calculator tool can simplify the process, saving you time and effort. By understanding the concept of vertex form and using a calculator tool, you can improve your understanding of parabolas and their real-world applications. So, the next time you encounter a parabola, remember to use a calculator tool to convert it to its vertex form.
What is the vertex form of a parabola?
+The vertex form of a parabola is y = a(x-h)^2 + k, where (h, k) is the vertex of the parabola.
How do I convert a parabola to its vertex form?
+To convert a parabola to its vertex form, complete the square by adding and subtracting (b/2a)^2 inside the parentheses.
What are the benefits of using a parabola to vertex form calculator tool?
+The benefits of using a parabola to vertex form calculator tool include saving time, reducing errors, and improving understanding.