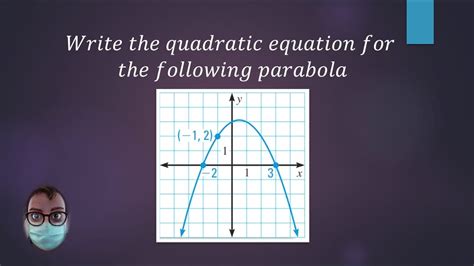
Parabolas are a fundamental concept in mathematics, particularly in algebra and geometry. One of the most important forms of a parabola is the intercept form, which provides valuable insights into its properties and behavior. In this article, we will delve into the world of parabolas in intercept form, exploring their definition, benefits, and practical applications.
What is a Parabola in Intercept Form?

A parabola in intercept form is a quadratic equation that represents a parabola in a unique way. The intercept form of a parabola is given by the equation:
y = a(x - p)(x - q)
where (p, 0) and (q, 0) are the x-intercepts of the parabola, and 'a' is a constant that determines the shape and direction of the parabola. The x-intercepts are the points where the parabola intersects the x-axis.
Benefits of Using Intercept Form
The intercept form of a parabola offers several benefits, including:
- Easy identification of x-intercepts: The intercept form clearly shows the x-intercepts of the parabola, which is essential for understanding its behavior and properties.
- Simplified calculations: The intercept form can simplify calculations, especially when dealing with quadratic equations.
- Geometric insights: The intercept form provides valuable geometric insights into the parabola, making it easier to visualize and analyze.
How to Find the Intercept Form of a Parabola

To find the intercept form of a parabola, follow these steps:
- Identify the x-intercepts: Find the points where the parabola intersects the x-axis. These points are the x-intercepts.
- Determine the constant 'a': Use the x-intercepts and the equation of the parabola to determine the value of 'a'.
- Write the intercept form: Use the x-intercepts and the value of 'a' to write the intercept form of the parabola.
Example: Finding the Intercept Form of a Parabola
Consider the quadratic equation:
y = x^2 + 4x + 4
To find the intercept form, follow these steps:
- Identify the x-intercepts: The x-intercepts are (-2, 0) and (-2, 0).
- Determine the constant 'a': Using the x-intercepts and the equation, we find that 'a' = 1.
- Write the intercept form: The intercept form is:
y = (x + 2)(x + 2)
Applications of Parabolas in Intercept Form

Parabolas in intercept form have numerous applications in various fields, including:
- Physics: Parabolas are used to model the trajectory of projectiles and the path of light.
- Engineering: Parabolas are used in the design of curves and surfaces.
- Computer Science: Parabolas are used in computer graphics and game development.
- Economics: Parabolas are used to model supply and demand curves.
Practical Example: Projectile Motion
Consider a projectile launched from the ground with an initial velocity of 20 m/s at an angle of 45°. The path of the projectile can be modeled using a parabola in intercept form.
y = (x - 20)(x + 20)
This equation represents the path of the projectile, with the x-intercepts representing the points where the projectile intersects the ground.
Conclusion and Next Steps
In conclusion, parabolas in intercept form are a powerful tool for understanding and analyzing quadratic equations. By recognizing the benefits and applications of intercept form, you can simplify calculations, gain geometric insights, and solve problems more efficiently. To further develop your skills, practice finding the intercept form of parabolas and explore their applications in various fields.
What are your thoughts on parabolas in intercept form? Share your experiences and insights in the comments below.