Matrix Calculator For Reduced Row Echelon Form Made Easy

Quick Links :

Introduction to Matrix Calculator for Reduced Row Echelon Form

In the world of linear algebra, matrices play a vital role in solving systems of equations. One of the most useful forms of a matrix is the Reduced Row Echelon Form (RREF), which allows us to easily identify the solutions to a system of linear equations. However, transforming a matrix into RREF can be a tedious and time-consuming process, especially for larger matrices. This is where a matrix calculator comes in handy. In this article, we will explore the concept of RREF, its importance, and how a matrix calculator can make the process easier.

What is Reduced Row Echelon Form (RREF)?

A matrix is said to be in Reduced Row Echelon Form (RREF) if it satisfies the following conditions:

• All rows consisting entirely of zeros are grouped together at the bottom of the matrix.
• Each row that is not entirely zeros has a 1 as its first nonzero entry (this entry is called a pivot).
• The column in which a pivot is located has all other entries as zeros.
• Each pivot is located to the right of the pivot in the row above it.

The RREF of a matrix is unique and can be obtained by performing a series of elementary row operations.

Importance of Reduced Row Echelon Form

The RREF of a matrix is essential in solving systems of linear equations. By transforming a matrix into RREF, we can easily identify the solutions to the system. The RREF also provides information about the consistency and independence of the system.

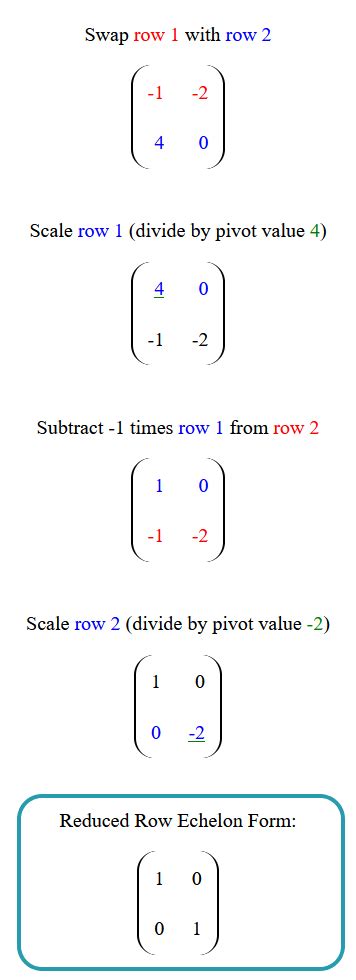
How to Transform a Matrix into Reduced Row Echelon Form

Transforming a matrix into RREF involves performing a series of elementary row operations. The steps involved are:

• Swap rows to ensure that the row with the most nonzero entries is at the top.
• Multiply a row by a scalar to ensure that the first nonzero entry is a 1.
• Add a multiple of one row to another row to eliminate nonzero entries below the pivot.
• Repeat the process until the entire matrix is in RREF.

Challenges in Transforming a Matrix into RREF

Transforming a matrix into RREF can be a time-consuming and error-prone process, especially for larger matrices. The process requires careful attention to detail and a thorough understanding of the elementary row operations.

Matrix Calculator for Reduced Row Echelon Form

A matrix calculator can simplify the process of transforming a matrix into RREF. A matrix calculator is a software tool that can perform various matrix operations, including transforming a matrix into RREF.

Benefits of Using a Matrix Calculator

Using a matrix calculator offers several benefits, including:

• Time-saving: A matrix calculator can perform the calculations much faster than a human.
• Accuracy: A matrix calculator eliminates the risk of human error.
• Ease of use: A matrix calculator is user-friendly and requires minimal input from the user.

How to Use a Matrix Calculator for Reduced Row Echelon Form

Using a matrix calculator is a straightforward process. Here are the steps involved:

• Enter the matrix into the calculator.
• Select the option to transform the matrix into RREF.
• The calculator will perform the calculations and display the RREF of the matrix.

Practical Applications of a Matrix Calculator

A matrix calculator has several practical applications, including:

• Solving systems of linear equations.
• Finding the inverse of a matrix.
• Performing linear transformations.

Conclusion

In conclusion, transforming a matrix into Reduced Row Echelon Form is an essential step in solving systems of linear equations. A matrix calculator can simplify the process and provide accurate results. Whether you are a student, teacher, or researcher, a matrix calculator is an indispensable tool in your mathematical toolkit.

Take Action

Try using a matrix calculator today and experience the ease and convenience of transforming matrices into Reduced Row Echelon Form. Share your experiences and tips with us in the comments section below.