Lines That Meet At 90 Degrees: Understanding Right Angles

Quick Links :

Lines that meet at 90 degrees are a fundamental concept in geometry and are known as right angles. Right angles play a crucial role in various aspects of mathematics, architecture, engineering, and design. In this article, we will delve into the world of right angles, exploring their definition, properties, and applications.

What are Right Angles?

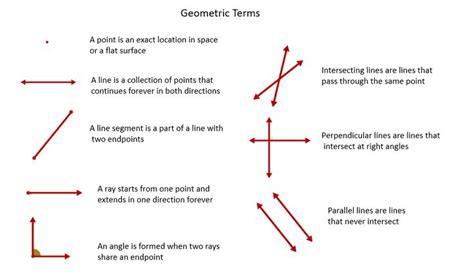
A right angle is formed when two lines intersect at a 90-degree angle. This means that the lines are perpendicular to each other, and the angle between them is exactly 90 degrees. Right angles are denoted by a square symbol (∟) or a 90-degree symbol (°). The concept of right angles is essential in geometry, as it helps to define various shapes, such as rectangles, squares, and triangles.

Properties of Right Angles

Right angles have several important properties that make them useful in various mathematical and real-world applications. Some of the key properties of right angles include:

• The sum of the angles in a right-angled triangle is always 180 degrees.
• The length of the hypotenuse (the side opposite the right angle) is always greater than the length of the other two sides.
• The area of a right-angled triangle can be calculated using the formula: Area = (base × height) / 2.

Applications of Right Angles

Right angles have numerous applications in various fields, including:

Architecture and Design

Right angles are used extensively in architecture and design to create symmetrical and balanced structures. Many buildings, bridges, and monuments feature right angles as a fundamental element of their design. Right angles also play a crucial role in the design of furniture, where they are used to create stable and functional pieces.

Engineering and Construction

Right angles are essential in engineering and construction, where they are used to ensure that structures are stable and secure. In construction, right angles are used to create square corners, which are critical in building foundations, walls, and roofs. Engineers also use right angles to design bridges, tunnels, and other infrastructure projects.

Types of Right Angles

There are several types of right angles, including:

• Acute right angle: An acute right angle is a right angle that is less than 90 degrees.
• Obtuse right angle: An obtuse right angle is a right angle that is greater than 90 degrees.
• Reflex right angle: A reflex right angle is a right angle that is greater than 180 degrees.

Real-World Examples of Right Angles

Right angles are ubiquitous in our daily lives, and we encounter them in various forms. Here are a few examples:

• Picture frames: Picture frames often feature right angles, which create a sense of balance and symmetry.
• Bookshelves: Bookshelves typically have right angles, which provide stability and support for the books.
• Staircases: Staircases feature right angles, which ensure that the stairs are safe and functional.

Conclusion

In conclusion, right angles are a fundamental concept in geometry and have numerous applications in various fields. Understanding right angles is essential for architects, engineers, designers, and anyone who works with shapes and structures. By recognizing the properties and applications of right angles, we can create more balanced, stable, and functional designs.

Call to Action

We hope this article has provided you with a comprehensive understanding of right angles. Whether you're an architect, engineer, or simply someone who appreciates geometry, we encourage you to share your thoughts and experiences with right angles in the comments section below. Don't forget to share this article with your friends and colleagues who might find it useful.