2 Ways Intersecting Chords Form Congruent Vertical Angles

Quick Links :

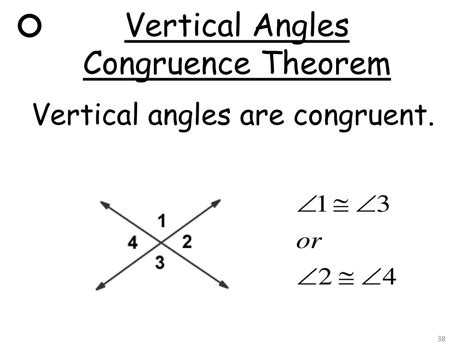
When two chords intersect inside a circle, they form a unique pair of angles known as vertical angles. These angles are not only interesting to observe, but they also have a special property that makes them congruent. In this article, we will explore the concept of intersecting chords and the formation of congruent vertical angles.

Understanding Intersecting Chords

Intersecting chords are two or more chords that cross each other inside a circle. This intersection point is called the point of intersection. When two chords intersect, they form four angles at the point of intersection. These angles are called vertical angles because they are opposite each other and form a straight line.

Formation of Vertical Angles

When two chords intersect, the angles formed at the point of intersection are vertical angles. Vertical angles are angles that are opposite each other and form a straight line. In the case of intersecting chords, the vertical angles are formed by the intersection of the two chords.

For example, let's consider two chords, AB and CD, that intersect at point E. The vertical angles formed at point E are ∠AEC and ∠BED. These angles are opposite each other and form a straight line.

Properties of Congruent Vertical Angles

One of the most interesting properties of intersecting chords is that the vertical angles formed are congruent. This means that the two angles are equal in measure. This property can be proven using the concept of inscribed angles.

An inscribed angle is an angle formed by two chords that intersect on the circle. When two chords intersect, the inscribed angles formed are equal in measure. Since vertical angles are formed by the intersection of two chords, they are also equal in measure, making them congruent.

Proof of Congruent Vertical Angles

To prove that vertical angles are congruent, we can use the concept of inscribed angles. Let's consider two chords, AB and CD, that intersect at point E. The vertical angles formed at point E are ∠AEC and ∠BED.

Since ∠AEC and ∠BED are inscribed angles, they are equal in measure. Therefore, we can conclude that ∠AEC ≅ ∠BED.

Real-World Applications of Congruent Vertical Angles

The concept of congruent vertical angles has several real-world applications. One of the most common applications is in the field of architecture. Architects use the concept of vertical angles to design buildings and bridges.

For example, when designing a bridge, architects use the concept of vertical angles to ensure that the bridge is stable and secure. By using congruent vertical angles, architects can create a strong and stable structure that can withstand various forces and loads.

Other Applications of Congruent Vertical Angles

Other applications of congruent vertical angles include:

• Engineering: Congruent vertical angles are used in engineering to design and build structures such as bridges, buildings, and roads.
• Physics: Congruent vertical angles are used in physics to study the motion of objects and the forces that act upon them.
• Art: Congruent vertical angles are used in art to create symmetry and balance in designs.

Conclusion and Final Thoughts

In conclusion, the concept of intersecting chords and congruent vertical angles is a fascinating topic in geometry. The properties of congruent vertical angles have several real-world applications, including architecture, engineering, physics, and art.

By understanding the concept of intersecting chords and congruent vertical angles, we can appreciate the beauty and complexity of geometry. Whether you are an architect, engineer, physicist, or artist, the concept of congruent vertical angles is an essential tool to have in your toolkit.

We hope this article has inspired you to learn more about geometry and its applications. Share your thoughts and comments below, and don't forget to share this article with your friends and colleagues.