Intercept Form Of A Parabola Made Easy

Quick Links :

Understanding the intercept form of a parabola can seem daunting at first, but with a clear and concise explanation, it can be made easy to grasp. In this article, we will break down the concept of intercept form of a parabola, its benefits, and provide practical examples to help you master this concept.

What is the Intercept Form of a Parabola?

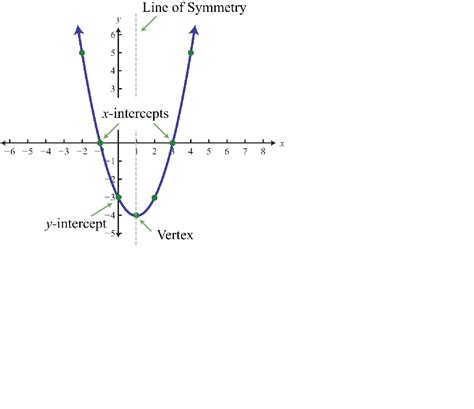
The intercept form of a parabola is a way of expressing the equation of a parabola in terms of its x and y intercepts. This form is particularly useful when we want to find the x and y intercepts of a parabola, as it allows us to read them directly from the equation. The intercept form of a parabola is given by:

y = a(x - p)(x - q)

where (p, 0) and (q, 0) are the x-intercepts of the parabola, and a is a constant that determines the direction and width of the parabola.

Benefits of the Intercept Form

The intercept form of a parabola has several benefits that make it a useful tool for solving problems in mathematics and physics. Some of the benefits include:

• Easy identification of x and y intercepts: The intercept form allows us to read the x and y intercepts directly from the equation, making it easier to identify them.
• Simplified calculations: The intercept form can simplify calculations when finding the x and y intercepts of a parabola.
• Clear visualization: The intercept form can help us visualize the parabola and its intercepts, making it easier to understand the behavior of the parabola.

How to Convert a Parabola to Intercept Form

Converting a parabola to intercept form is a straightforward process that involves factoring the quadratic expression. Here are the steps:

1. Factor the quadratic expression: Factor the quadratic expression into the product of two binomials.
2. Identify the x-intercepts: Identify the x-intercepts from the factored form of the quadratic expression.
3. Write the equation in intercept form: Write the equation in intercept form using the x-intercepts and the constant a.

Example: Converting a Parabola to Intercept Form

Find the intercept form of the parabola y = x^2 + 4x + 3.

Solution:

1. Factor the quadratic expression: x^2 + 4x + 3 = (x + 1)(x + 3)
2. Identify the x-intercepts: (-1, 0) and (-3, 0)
3. Write the equation in intercept form: y = (x + 1)(x + 3)

Applications of the Intercept Form

The intercept form of a parabola has several applications in mathematics and physics. Some of the applications include:

• Finding the x and y intercepts of a parabola
• Graphing parabolas
• Solving quadratic equations
• Modeling real-world phenomena, such as the trajectory of a projectile

Example: Finding the x and y Intercepts of a Parabola

Find the x and y intercepts of the parabola y = 2(x - 1)(x - 3).

Solution:

The x-intercepts are (1, 0) and (3, 0). To find the y-intercept, substitute x = 0 into the equation:

y = 2(0 - 1)(0 - 3) y = 6

Therefore, the y-intercept is (0, 6).

Conclusion: Mastering the Intercept Form

In conclusion, the intercept form of a parabola is a powerful tool for solving problems in mathematics and physics. By understanding how to convert a parabola to intercept form and applying it to real-world problems, you can master this concept and take your problem-solving skills to the next level.

We hope this article has helped you understand the intercept form of a parabola and its applications. If you have any questions or need further clarification, please don't hesitate to ask.