5 Steps To Write A Function In Standard Form

Quick Links :

Writing a function in standard form is a crucial skill in mathematics, particularly in algebra and calculus. It allows us to express a function in a way that makes it easy to analyze and manipulate. In this article, we will explore the 5 steps to write a function in standard form.

Understanding the Importance of Standard Form

Writing a function in standard form is essential because it provides a clear and concise way to express a function. It allows us to easily identify the key features of the function, such as its zeros, vertex, and axis of symmetry. Moreover, standard form makes it easier to compare and contrast different functions.

What is Standard Form?

Standard form is a way of expressing a function in the form f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. This form is also known as vertex form. The standard form provides a clear and concise way to express a function, making it easy to analyze and manipulate.

Step 1: Identify the Vertex

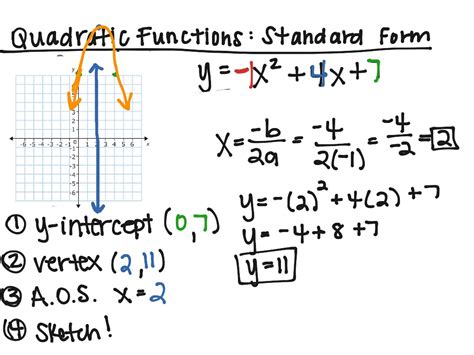
The first step in writing a function in standard form is to identify the vertex. The vertex is the point where the parabola changes direction. To find the vertex, we need to find the x-coordinate of the vertex, which is given by the formula x = -b / 2a.

Example: Finding the Vertex

Suppose we have the function f(x) = x^2 + 4x + 4. To find the vertex, we need to find the x-coordinate of the vertex. Using the formula x = -b / 2a, we get x = -4 / 2(1) = -2.

Step 2: Rewrite the Function in Vertex Form

Once we have identified the vertex, we can rewrite the function in vertex form. The vertex form is given by f(x) = a(x - h)^2 + k, where (h, k) is the vertex.

Example: Rewriting the Function in Vertex Form

Using the vertex we found in Step 1, we can rewrite the function f(x) = x^2 + 4x + 4 in vertex form as f(x) = (x + 2)^2 - 4.

Step 3: Identify the Value of 'a'

The value of 'a' is the coefficient of the squared term in the function. In the vertex form, 'a' is the coefficient of the (x - h)^2 term.

Example: Finding the Value of 'a'

In the function f(x) = (x + 2)^2 - 4, the value of 'a' is 1.

Step 4: Identify the Value of 'h' and 'k'

The values of 'h' and 'k' are the coordinates of the vertex. In the vertex form, 'h' is the x-coordinate of the vertex, and 'k' is the y-coordinate.

Example: Finding the Values of 'h' and 'k'

In the function f(x) = (x + 2)^2 - 4, the value of 'h' is -2, and the value of 'k' is -4.

Step 5: Write the Function in Standard Form

Using the values of 'a', 'h', and 'k', we can write the function in standard form.

Example: Writing the Function in Standard Form

Using the values of 'a', 'h', and 'k', we can write the function f(x) = (x + 2)^2 - 4 in standard form as f(x) = 1(x + 2)^2 - 4.

By following these 5 steps, we can write a function in standard form. Writing a function in standard form is essential in mathematics, particularly in algebra and calculus. It provides a clear and concise way to express a function, making it easy to analyze and manipulate.