Convert Vertex Form To Factored Form Easily

Quick Links :

Understanding the Importance of Converting Vertex Form to Factored Form

Converting vertex form to factored form is a crucial skill in algebra, as it allows us to easily identify the roots and the vertex of a quadratic function. In this article, we will explore the benefits of converting vertex form to factored form, the steps involved in the process, and provide practical examples to illustrate the concept.

What is Vertex Form?

Vertex form is a way of expressing a quadratic function in the form f(x) = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola. This form is useful for identifying the vertex and the axis of symmetry of the parabola.

What is Factored Form?

Factored form is a way of expressing a quadratic function in the form f(x) = a(x - r)(x - s), where r and s are the roots of the quadratic function. This form is useful for identifying the roots and the factors of the quadratic function.

Why Convert Vertex Form to Factored Form?

Converting vertex form to factored form has several benefits:

• Easily identify the roots of the quadratic function
• Factor the quadratic function easily
• Solve quadratic equations easily
• Graph the quadratic function easily

Steps to Convert Vertex Form to Factored Form

Converting vertex form to factored form involves the following steps:

1. Identify the vertex (h, k) of the quadratic function
2. Identify the value of 'a' in the vertex form
3. Use the formula x = h ± √(-a) to find the roots of the quadratic function
4. Use the roots to write the factored form of the quadratic function

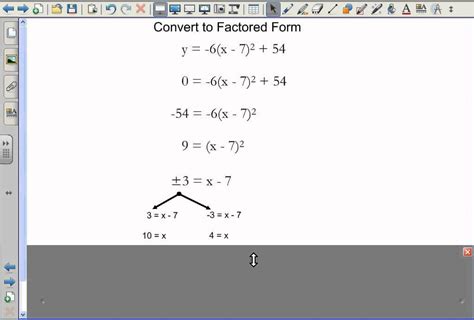
Example 1: Convert Vertex Form to Factored Form

f(x) = -(x - 2)^2 + 3

To convert this to factored form, we need to find the roots of the quadratic function.

x = 2 ± √(-(-1)) x = 2 ± √1 x = 2 ± 1

So, the roots are x = 1 and x = 3.

Using the roots, we can write the factored form of the quadratic function:

f(x) = -(x - 1)(x - 3)

Example 2: Convert Vertex Form to Factored Form

f(x) = 2(x + 1)^2 - 4

To convert this to factored form, we need to find the roots of the quadratic function.

x = -1 ± √(-2) x = -1 ± √(-2) x = -1 ± i√2

So, the roots are x = -1 + i√2 and x = -1 - i√2.

Using the roots, we can write the factored form of the quadratic function:

f(x) = 2(x + 1 + i√2)(x + 1 - i√2)

Common Mistakes to Avoid When Converting Vertex Form to Factored Form

When converting vertex form to factored form, there are several common mistakes to avoid:

• Forgetting to identify the value of 'a' in the vertex form
• Forgetting to use the formula x = h ± √(-a) to find the roots
• Forgetting to use the roots to write the factored form

Conclusion and Next Steps

Converting vertex form to factored form is an essential skill in algebra. By following the steps outlined in this article, you can easily convert vertex form to factored form and identify the roots and factors of quadratic functions. Practice converting different quadratic functions to factored form to become more proficient in this skill.

We encourage you to try converting different vertex forms to factored forms and share your results in the comments section. If you have any questions or need further clarification, please don't hesitate to ask.