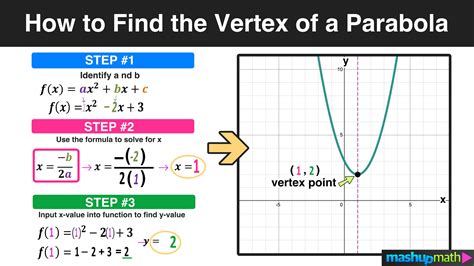
Finding the x-intercept of a quadratic equation in vertex form is a crucial skill in algebra and graphing. The x-intercept is the point where the graph of the equation crosses the x-axis, and it's essential to understand how to find it efficiently. In this article, we'll explore the concept of vertex form, its significance, and provide a step-by-step guide on how to find the x-intercept with ease.
What is Vertex Form?
The vertex form of a quadratic equation is a way of expressing a quadratic function in the form f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. This form is particularly useful for graphing and analyzing quadratic functions, as it provides valuable information about the shape and position of the parabola.

Importance of Vertex Form
The vertex form is a powerful tool in algebra and graphing, offering several benefits:
- Easy graphing: The vertex form allows you to quickly identify the vertex of the parabola, making it simple to graph the function.
- Analysis of shape: By examining the value of
a, you can determine the direction and width of the parabola. - Finding x-intercepts: As we'll discuss in this article, the vertex form provides a straightforward method for finding the x-intercepts of a quadratic equation.
Finding the X-Intercept of a Quadratic Equation in Vertex Form
To find the x-intercept of a quadratic equation in vertex form, follow these steps:
Step 1: Identify the Vertex Form of the Equation
The vertex form of a quadratic equation is f(x) = a(x - h)^2 + k. Identify the values of a, h, and k in the given equation.

Step 2: Set the Equation Equal to Zero
To find the x-intercept, set the equation equal to zero: f(x) = 0. This will give you the equation a(x - h)^2 + k = 0.
Step 3: Subtract k from Both Sides
Subtract k from both sides of the equation to isolate the squared term: a(x - h)^2 = -k.
Step 4: Divide Both Sides by a
Divide both sides of the equation by a to solve for (x - h)^2: (x - h)^2 = -k/a.
Step 5: Take the Square Root of Both Sides
Take the square root of both sides of the equation to solve for x - h: x - h = ±√(-k/a).
Step 6: Add h to Both Sides
Add h to both sides of the equation to solve for x: x = h ± √(-k/a).
Example: Finding the X-Intercept of a Quadratic Equation in Vertex Form
Suppose we have the quadratic equation f(x) = 2(x - 3)^2 + 5. To find the x-intercept, follow the steps above:
- Identify the vertex form:
f(x) = 2(x - 3)^2 + 5 - Set the equation equal to zero:
2(x - 3)^2 + 5 = 0 - Subtract 5 from both sides:
2(x - 3)^2 = -5 - Divide both sides by 2:
(x - 3)^2 = -5/2 - Take the square root of both sides:
x - 3 = ±√(-5/2) - Add 3 to both sides:
x = 3 ± √(-5/2)
The x-intercepts of the quadratic equation are x = 3 ± √(-5/2).
Practical Applications of Finding X-Intercepts
Finding the x-intercepts of a quadratic equation has numerous practical applications in various fields, including:
- Physics and engineering: X-intercepts are used to determine the position and velocity of objects in motion.
- Economics: X-intercepts are used to analyze the behavior of supply and demand curves.
- Computer science: X-intercepts are used in algorithms for solving quadratic equations and optimizing functions.
Conclusion
Finding the x-intercept of a quadratic equation in vertex form is a straightforward process that requires identifying the vertex form, setting the equation equal to zero, and solving for x. By following these steps, you can easily find the x-intercept of any quadratic equation in vertex form. Whether you're a student, teacher, or professional, understanding how to find x-intercepts is an essential skill that will serve you well in various mathematical and real-world applications.

FAQ Section
What is the vertex form of a quadratic equation?
+The vertex form of a quadratic equation is f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola.
Why is finding the x-intercept important?
+Finding the x-intercept is important because it provides valuable information about the shape and position of the parabola, and has numerous practical applications in various fields.
Can I find the x-intercept of a quadratic equation in standard form?
+Yes, you can find the x-intercept of a quadratic equation in standard form by factoring or using the quadratic formula. However, the vertex form provides a more straightforward method for finding the x-intercept.
Take Action
Now that you've learned how to find the x-intercept of a quadratic equation in vertex form, practice applying this skill to different equations and explore its practical applications in various fields. Share your thoughts and questions in the comments below, and don't forget to share this article with your friends and colleagues!