Convert Standard Form To Point Slope Form In 5 Steps

Quick Links :

Understanding the Importance of Converting Standard Form to Point Slope Form

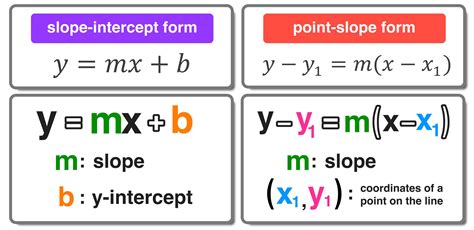
In mathematics, particularly in algebra and geometry, linear equations play a vital role in solving problems. Linear equations can be represented in various forms, each serving a specific purpose. Among these forms, the standard form and point slope form are two of the most commonly used representations. The standard form of a linear equation is typically represented as ax + by = c, where a, b, and c are constants. On the other hand, the point slope form is represented as y - y1 = m(x - x1), where m is the slope and (x1, y1) is a point on the line. In this article, we will explore the importance of converting standard form to point slope form and provide a step-by-step guide on how to do it.

The ability to convert standard form to point slope form is essential in various mathematical applications. For instance, when dealing with linear equations, it is often necessary to find the slope and a point on the line. The point slope form provides a clear representation of the slope and a point on the line, making it easier to work with. Additionally, converting standard form to point slope form can help simplify complex equations and make them more manageable.

The Benefits of Converting Standard Form to Point Slope Form

Converting standard form to point slope form offers several benefits, including:

• Simplified equations: Point slope form can simplify complex equations by providing a clear representation of the slope and a point on the line.
• Easier graphing: With the point slope form, graphing linear equations becomes more straightforward, as the slope and a point on the line are clearly defined.
• Improved problem-solving: The point slope form can facilitate problem-solving by providing a clear understanding of the slope and a point on the line.

Step-by-Step Guide to Converting Standard Form to Point Slope Form

Converting standard form to point slope form involves a few simple steps. Here's a step-by-step guide:

Step 1: Identify the Standard Form Equation

Begin by identifying the standard form equation, which is typically represented as ax + by = c. Take note of the coefficients a, b, and c, as they will be used in the subsequent steps.

Step 2: Solve for y

To convert the standard form equation to point slope form, we need to solve for y. This involves isolating y on one side of the equation. To do this, subtract the term with x from both sides of the equation, and then divide both sides by the coefficient of y.

Step 3: Identify the Slope (m)

The slope (m) can be determined from the coefficient of x in the equation. The slope is simply the negative reciprocal of the coefficient of x.

Step 4: Find a Point on the Line (x1, y1)

To find a point on the line, we can substitute a value for x into the equation and solve for y. Alternatively, we can use the coefficients a, b, and c to find a point on the line.

Step 5: Write the Point Slope Form Equation

Using the slope (m) and the point on the line (x1, y1), we can write the point slope form equation as y - y1 = m(x - x1).

Example: Converting Standard Form to Point Slope Form

Suppose we have the standard form equation 2x + 3y = 5. To convert this to point slope form, we can follow the steps outlined above.

• Step 1: Identify the standard form equation: 2x + 3y = 5
• Step 2: Solve for y: 3y = -2x + 5; y = (-2/3)x + 5/3
• Step 3: Identify the slope (m): m = -2/3
• Step 4: Find a point on the line (x1, y1): (0, 5/3)
• Step 5: Write the point slope form equation: y - 5/3 = (-2/3)(x - 0)

Conclusion

In conclusion, converting standard form to point slope form is a valuable skill in mathematics, particularly in algebra and geometry. By following the steps outlined in this article, you can easily convert standard form equations to point slope form. Remember to identify the standard form equation, solve for y, identify the slope, find a point on the line, and write the point slope form equation.

We hope this article has been informative and helpful in your mathematical endeavors. If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and experiences in the comments section below.