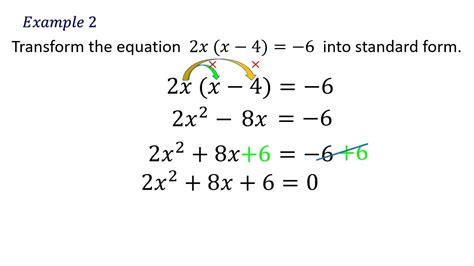5 Ways To Convert Quadratic To Standard Form

Quick Links :

Converting quadratic equations to standard form is a fundamental concept in algebra that has numerous practical applications in physics, engineering, and other fields. Quadratic equations can be represented in various forms, but standard form, also known as the general form, is a widely used and accepted format. In this article, we will explore five ways to convert quadratic equations to standard form.

Quadratic equations are polynomial equations of degree two, which means the highest power of the variable (usually x) is two. These equations can be written in different forms, such as vertex form, factored form, and standard form. While vertex form is useful for graphing and identifying key features of the parabola, standard form is more commonly used in algebraic manipulations and solving quadratic equations.

Converting quadratic equations to standard form is essential because it allows us to easily identify the coefficients of the equation, which are crucial in solving the equation using various methods, such as factoring, quadratic formula, or graphing. Moreover, standard form is often required when solving systems of equations, where quadratic equations are involved.

What is Standard Form?

Standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. The coefficient 'a' represents the coefficient of the squared term, 'b' represents the coefficient of the linear term, and 'c' represents the constant term.

Why Convert to Standard Form?

Converting quadratic equations to standard form has several advantages:

• Easily identifies the coefficients of the equation
• Allows for straightforward algebraic manipulations
• Facilitates solving quadratic equations using various methods
• Required for solving systems of equations involving quadratic equations

Method 1: Expanding the Expression

One way to convert a quadratic equation to standard form is by expanding the expression. This method involves multiplying out the terms and combining like terms.

For example, let's consider the quadratic equation (x + 3)(x - 4) = 0. To convert this to standard form, we can expand the expression by multiplying out the terms:

(x + 3)(x - 4) = x^2 - 4x + 3x - 12

Combine like terms:

x^2 - x - 12 = 0

This is the standard form of the quadratic equation.

Method 2: Rearranging the Terms

Another method for converting a quadratic equation to standard form is by rearranging the terms. This involves reordering the terms so that the equation is in the standard form ax^2 + bx + c = 0.

For example, consider the quadratic equation x^2 - 12 = -x. To convert this to standard form, we can rearrange the terms:

x^2 + x - 12 = 0

This is the standard form of the quadratic equation.

Method 3: Factoring Out the Greatest Common Factor

Factoring out the greatest common factor (GCF) is another method for converting a quadratic equation to standard form. This involves factoring out the largest factor that divides all the terms.

For example, consider the quadratic equation 2x^2 + 6x + 8 = 0. To convert this to standard form, we can factor out the GCF:

2(x^2 + 3x + 4) = 0

This is the standard form of the quadratic equation.

Method 4: Using the Quadratic Formula

The quadratic formula is another method for converting a quadratic equation to standard form. This involves using the formula x = (-b ± √(b^2 - 4ac)) / 2a to solve the equation.

For example, consider the quadratic equation x^2 + 5x + 6 = 0. To convert this to standard form, we can use the quadratic formula:

x = (-5 ± √(5^2 - 4(1)(6))) / 2(1)

x = (-5 ± √(25 - 24)) / 2

x = (-5 ± √1) / 2

x = (-5 ± 1) / 2

This gives us two possible solutions: x = -2 and x = -3. We can then write the equation in standard form:

(x + 2)(x + 3) = 0

This is the standard form of the quadratic equation.

Method 5: Using Graphing

Graphing is another method for converting a quadratic equation to standard form. This involves graphing the equation on a coordinate plane and then writing the equation in standard form based on the graph.

For example, consider the quadratic equation x^2 - 4x - 3 = 0. To convert this to standard form, we can graph the equation on a coordinate plane:

The graph shows that the equation is a parabola that opens upward. We can then write the equation in standard form:

x^2 - 4x - 3 = 0

This is the standard form of the quadratic equation.

In conclusion, converting quadratic equations to standard form is an essential skill in algebra. There are five methods for doing so: expanding the expression, rearranging the terms, factoring out the greatest common factor, using the quadratic formula, and using graphing. By mastering these methods, you can easily convert quadratic equations to standard form and solve them using various techniques.