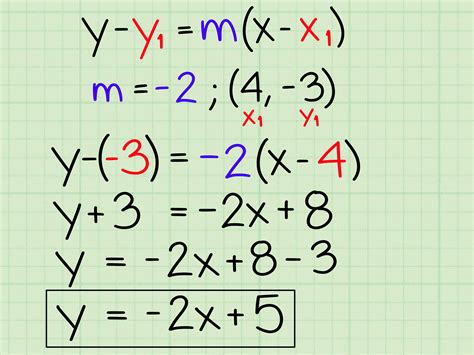3 Easy Steps To Convert Equations To Slope Intercept Form

Quick Links :

Converting equations to slope-intercept form is a fundamental skill in algebra and mathematics. Slope-intercept form, also known as y = mx + b form, is a way of expressing linear equations in a simple and intuitive way. In this article, we will explore the importance of converting equations to slope-intercept form and provide a step-by-step guide on how to do it.

Converting equations to slope-intercept form is essential in mathematics because it allows us to easily identify the slope and y-intercept of a line. The slope-intercept form is also useful in graphing lines, solving systems of equations, and modeling real-world problems. Moreover, understanding how to convert equations to slope-intercept form can help students develop problem-solving skills, critical thinking, and analytical reasoning.

In this article, we will provide a comprehensive guide on how to convert equations to slope-intercept form in three easy steps. We will also include examples, illustrations, and explanations to help students understand the concept better.

What is Slope-Intercept Form?

Slope-intercept form is a way of expressing linear equations in the form y = mx + b, where:

• m is the slope of the line (a measure of how steep the line is)
• b is the y-intercept (the point where the line crosses the y-axis)
• x is the independent variable (the input or x-value)
• y is the dependent variable (the output or y-value)

Step 1: Identify the Equation

The first step in converting an equation to slope-intercept form is to identify the equation. This may seem obvious, but it's essential to understand the structure of the equation and the variables involved. Look for the variables x and y, and identify the coefficients and constants.

For example, let's consider the equation:

2x + 3y = 7

In this equation, x and y are the variables, 2 and 3 are the coefficients, and 7 is the constant.

Example:

Identify the equation: 4x - 2y = 11

In this equation, x and y are the variables, 4 and -2 are the coefficients, and 11 is the constant.

Step 2: Isolate the Variable y

The second step is to isolate the variable y. This involves rearranging the equation to solve for y. Use algebraic manipulations such as addition, subtraction, multiplication, or division to isolate y.

For example, let's consider the equation:

2x + 3y = 7

To isolate y, we need to subtract 2x from both sides and then divide by 3:

3y = 7 - 2x y = (7 - 2x) / 3

Example:

Isolate the variable y: 4x - 2y = 11

To isolate y, we need to add 2y to both sides and then divide by -2:

-2y = 11 - 4x y = (4x - 11) / -2 y = -2x + 11/2

Step 3: Simplify the Equation

The final step is to simplify the equation. This involves combining like terms and expressing the equation in the simplest form possible.

For example, let's consider the equation:

y = (7 - 2x) / 3

This equation is already in the simplest form. However, we can express it in a more intuitive way by rewriting it as:

y = -2/3x + 7/3

Example:

Simplify the equation: y = -2x + 11/2

This equation is already in the simplest form.

Conclusion

In conclusion, converting equations to slope-intercept form is a straightforward process that involves identifying the equation, isolating the variable y, and simplifying the equation. By following these three easy steps, you can easily convert any linear equation to slope-intercept form. Remember to practice, practice, practice to become proficient in converting equations to slope-intercept form.