Standard Form Of A Circle: Homework 9 Made Easy

Quick Links :

The standard form of a circle is a fundamental concept in mathematics, particularly in geometry and algebra. It's a crucial topic to grasp, as it has numerous applications in various fields, such as physics, engineering, and computer graphics. In this article, we'll delve into the world of circles, exploring the standard form equation, its components, and how to work with it.

What is the Standard Form of a Circle?

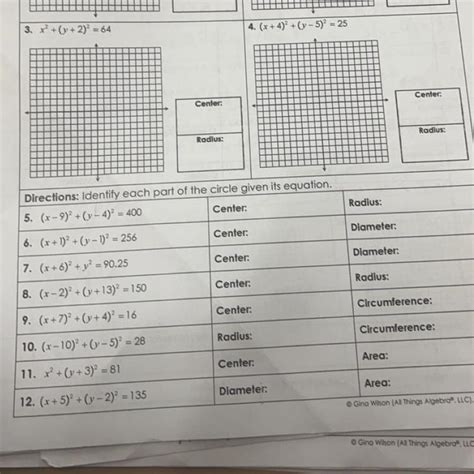
The standard form of a circle is a mathematical equation that describes the shape and size of a circle. It's a quadratic equation in two variables, x and y, which represents the set of all points that are equidistant from a fixed central point, called the center. The standard form equation of a circle is given by:

(x - h)^2 + (y - k)^2 = r^2

where (h, k) represents the coordinates of the center, and r is the radius of the circle.

Understanding the Components of the Standard Form Equation

To work with the standard form equation, it's essential to understand its components:

• (h, k) represents the coordinates of the center of the circle. The center is the fixed point from which the distance to any point on the circle is measured.
• r is the radius of the circle, which is the distance from the center to any point on the circle.
• (x - h)^2 and (y - k)^2 represent the squared differences between the x and y coordinates of a point on the circle and the x and y coordinates of the center.

How to Write a Circle Equation in Standard Form

Writing a circle equation in standard form involves identifying the center and radius of the circle. Here's a step-by-step guide:

1. Identify the center of the circle: Determine the coordinates of the center (h, k).
2. Determine the radius: Find the distance from the center to any point on the circle.
3. Plug in the values: Substitute the values of h, k, and r into the standard form equation.

Example: Write the equation of a circle with center (2, 3) and radius 4.

(x - 2)^2 + (y - 3)^2 = 4^2

Simplifying, we get:

(x - 2)^2 + (y - 3)^2 = 16

Graphing a Circle in Standard Form

Graphing a circle in standard form involves plotting the center and radius of the circle on a coordinate plane. Here's a step-by-step guide:

1. Plot the center: Mark the coordinates of the center (h, k) on the coordinate plane.
2. Plot the radius: Draw a circle with radius r, centered at (h, k).

Example: Graph the equation (x - 2)^2 + (y - 3)^2 = 16.

Tips and Tricks for Working with Circles in Standard Form

Here are some tips and tricks for working with circles in standard form:

• To find the center of a circle, look for the values of h and k in the equation.
• To find the radius, take the square root of the constant term (r^2).
• To graph a circle, plot the center and radius on a coordinate plane.

By mastering the standard form of a circle, you'll be able to work with circles with ease and confidence. Remember to practice, practice, practice, and you'll become a pro at working with circles in no time!

Real-World Applications of Circles

Circles have numerous real-world applications, including:

• Architecture: Circles are used in the design of buildings, bridges, and other structures.
• Engineering: Circles are used in the design of wheels, gears, and other mechanical systems.
• Physics: Circles are used to describe the motion of objects in circular paths.

Conclusion

In conclusion, the standard form of a circle is a fundamental concept in mathematics that has numerous applications in various fields. By understanding the standard form equation, its components, and how to work with it, you'll be able to solve problems and graph circles with ease and confidence. Remember to practice, practice, practice, and you'll become a pro at working with circles in no time!

We hope this article has been helpful in your journey to mastering circles in standard form. If you have any questions or comments, please feel free to share them below.