Mastering Quadratics: Graphing In Vertex Form Made Easy

Quick Links :

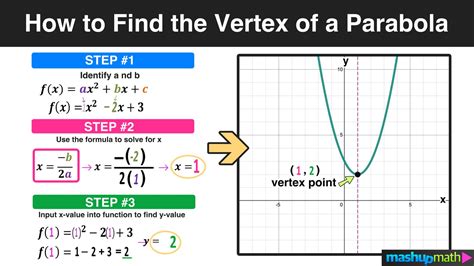
The quadratic equation - a fundamental concept in algebra that has been a cornerstone of mathematics for centuries. One of the most essential skills in mastering quadratics is graphing in vertex form, a crucial technique that enables students to visualize and analyze these complex equations with ease. In this article, we'll delve into the world of vertex form graphing, exploring its importance, benefits, and step-by-step instructions on how to master this skill.

Graphing in vertex form is a powerful tool that allows students to identify key characteristics of a quadratic equation, such as its vertex, axis of symmetry, and maximum or minimum values. By rewriting a quadratic equation in vertex form, students can easily determine the shape and orientation of the parabola, making it an indispensable technique in solving problems and modeling real-world applications.

Understanding Vertex Form

Vertex form, also known as the vertex representation, is a way of expressing a quadratic equation in the form:

f(x) = a(x - h)^2 + k

where (h, k) represents the vertex of the parabola. The vertex is the lowest or highest point on the parabola, and it plays a crucial role in determining the shape and orientation of the curve.

Why is Vertex Form Important?

Vertex form is essential in graphing quadratics because it provides a clear and concise way to identify key characteristics of the equation. By rewriting a quadratic equation in vertex form, students can easily determine the:

• Vertex (h, k)
• Axis of symmetry (x = h)
• Maximum or minimum value (f(h) = k)
• Opening direction (a > 0 for upward-facing, a < 0 for downward-facing)

Converting to Vertex Form

To convert a quadratic equation to vertex form, students can use the following steps:

1. Complete the square: Rewrite the quadratic equation in the form ax^2 + bx + c = 0.
2. Move the constant term: Move the constant term to the right-hand side of the equation.
3. Factor out the coefficient: Factor out the coefficient of the squared term.
4. Find the vertex: Identify the vertex (h, k) by setting the squared term equal to zero.

Example: Converting to Vertex Form

Suppose we want to convert the quadratic equation x^2 + 6x + 8 = 0 to vertex form. We can follow the steps above to get:

x^2 + 6x + 8 = 0 x^2 + 6x = -8 x^2 + 6x + 9 = -8 + 9 (x + 3)^2 = 1 f(x) = (x + 3)^2 - 1

The vertex form of the equation is f(x) = (x + 3)^2 - 1, with a vertex at (-3, -1).

Graphing in Vertex Form

Once a quadratic equation is rewritten in vertex form, graphing becomes a straightforward process. Students can use the following steps to graph the equation:

1. Plot the vertex: Plot the vertex (h, k) on the coordinate plane.
2. Determine the axis of symmetry: Draw a vertical line through the vertex to represent the axis of symmetry.
3. Determine the opening direction: If a > 0, the parabola opens upward; if a < 0, the parabola opens downward.
4. Plot additional points: Plot additional points on either side of the vertex to complete the graph.

Example: Graphing in Vertex Form

Suppose we want to graph the quadratic equation f(x) = (x + 3)^2 - 1. We can follow the steps above to get:

Vertex: (-3, -1) Axis of symmetry: x = -3 Opening direction: Upward-facing (a > 0)

Plotting the vertex and additional points on either side, we can complete the graph of the parabola.

Benefits of Graphing in Vertex Form

Graphing in vertex form offers several benefits, including:

• Easy identification of key characteristics (vertex, axis of symmetry, maximum or minimum value)
• Clear visualization of the parabola's shape and orientation
• Simplified analysis of quadratic equations and their applications

Common Applications of Vertex Form

Vertex form has numerous applications in various fields, including:

• Physics: Modeling the trajectory of projectiles and the behavior of oscillating systems
• Engineering: Designing and optimizing systems, such as bridges and electronic circuits
• Economics: Modeling supply and demand curves and optimizing production costs

Conclusion and Next Steps

Mastering graphing in vertex form is a crucial skill in algebra that can help students solve problems and model real-world applications with ease. By understanding the importance of vertex form, converting equations to vertex form, and graphing in vertex form, students can gain a deeper appreciation for the power and versatility of quadratic equations.

We hope this article has provided a comprehensive guide to graphing in vertex form. Do you have any questions or topics you'd like to discuss? Share your thoughts in the comments below!