5 Ways To Master Graphing From Factored Form

Quick Links :

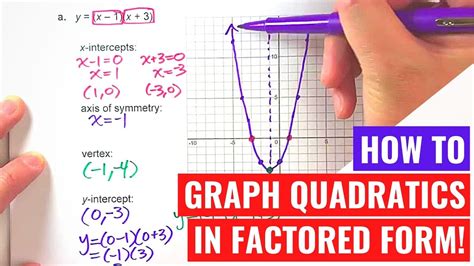
Graphing from factored form is a fundamental skill in algebra that can be challenging to master, but with the right strategies and practice, anyone can become proficient. Factored form is a way of expressing a quadratic equation in a format that makes it easier to identify the roots, or solutions, of the equation. In this article, we'll explore five ways to master graphing from factored form, and provide practical examples and tips to help you improve your skills.

Understanding the Basics of Factored Form

To master graphing from factored form, it's essential to understand the basics of factored form. A quadratic equation in factored form is written as:

y = a(x - r)(x - s)

where a is a constant, and r and s are the roots of the equation. The roots are the values of x that make the equation true. When we graph a quadratic equation in factored form, the graph will be a parabola that opens upwards or downwards, depending on the value of a.

How to Identify the Roots of a Quadratic Equation

To identify the roots of a quadratic equation, we need to set the equation equal to zero and solve for x. For example, if we have the equation:

y = (x - 2)(x + 3)

We can set y equal to zero and solve for x:

0 = (x - 2)(x + 3)

This gives us two possible solutions:

x - 2 = 0 or x + 3 = 0

Solving for x, we get:

x = 2 or x = -3

These are the roots of the equation.

Method 1: Using the Roots to Graph the Parabola

One way to master graphing from factored form is to use the roots to graph the parabola. To do this, we need to identify the roots of the equation, as we did in the previous section. Once we have the roots, we can use them to determine the shape of the parabola.

For example, if we have the equation:

y = (x - 2)(x + 3)

We know that the roots are x = 2 and x = -3. We can use these roots to graph the parabola by plotting the points (2, 0) and (-3, 0) on the coordinate plane. We can then draw a smooth curve through these points to create the parabola.

Tips for Graphing from Roots

Here are some tips for graphing from roots:

• Make sure to plot the roots accurately on the coordinate plane.
• Use a smooth curve to connect the roots, rather than a series of straight lines.
• If the roots are close together, use a smaller scale on the coordinate plane to ensure accuracy.

Method 2: Using the Vertex to Graph the Parabola

Another way to master graphing from factored form is to use the vertex to graph the parabola. The vertex is the lowest or highest point on the parabola, and it can be found using the formula:

x = -b / 2a

where a and b are the coefficients of the quadratic equation.

For example, if we have the equation:

y = (x - 2)(x + 3)

We can rewrite this equation in standard form:

y = x^2 + x - 6

Using the formula, we can find the vertex:

x = -1 / (2 * 1) = -1/2

Substituting this value back into the equation, we can find the y-coordinate of the vertex:

y = (-1/2)^2 + (-1/2) - 6 = -25/4

So, the vertex is at the point (-1/2, -25/4).

Tips for Graphing from the Vertex

Here are some tips for graphing from the vertex:

• Make sure to calculate the vertex accurately using the formula.
• Use the vertex to determine the direction of the parabola (i.e., whether it opens upwards or downwards).
• Use a smooth curve to connect the vertex to the roots, rather than a series of straight lines.

Method 3: Using the Axis of Symmetry to Graph the Parabola

Another way to master graphing from factored form is to use the axis of symmetry to graph the parabola. The axis of symmetry is a vertical line that passes through the vertex of the parabola, and it divides the parabola into two equal halves.

For example, if we have the equation:

y = (x - 2)(x + 3)

We can rewrite this equation in standard form:

y = x^2 + x - 6

Using the formula, we can find the axis of symmetry:

x = -b / 2a = -1 / (2 * 1) = -1/2

This means that the axis of symmetry is the vertical line x = -1/2.

Tips for Graphing from the Axis of Symmetry

Here are some tips for graphing from the axis of symmetry:

• Make sure to calculate the axis of symmetry accurately using the formula.
• Use the axis of symmetry to determine the direction of the parabola (i.e., whether it opens upwards or downwards).
• Use a smooth curve to connect the axis of symmetry to the roots, rather than a series of straight lines.

Method 4: Using the Factored Form to Identify the Zeros of the Parabola

Another way to master graphing from factored form is to use the factored form to identify the zeros of the parabola. The zeros of a quadratic equation are the values of x that make the equation true.

For example, if we have the equation:

y = (x - 2)(x + 3)

We can set y equal to zero and solve for x:

0 = (x - 2)(x + 3)

This gives us two possible solutions:

x - 2 = 0 or x + 3 = 0

Solving for x, we get:

x = 2 or x = -3

These are the zeros of the equation.

Tips for Graphing from Zeros

Here are some tips for graphing from zeros:

• Make sure to solve the equation accurately to find the zeros.
• Use the zeros to determine the shape of the parabola (i.e., whether it opens upwards or downwards).
• Use a smooth curve to connect the zeros, rather than a series of straight lines.

Method 5: Using Technology to Graph the Parabola

Finally, another way to master graphing from factored form is to use technology to graph the parabola. There are many graphing calculators and software programs available that can help you graph quadratic equations quickly and accurately.

For example, if we have the equation:

y = (x - 2)(x + 3)

We can enter this equation into a graphing calculator or software program, and it will graph the parabola for us.

Tips for Graphing with Technology

Here are some tips for graphing with technology:

• Make sure to enter the equation accurately into the calculator or software program.
• Use the calculator or software program to explore the graph and identify its features (e.g., vertex, axis of symmetry, zeros).
• Use the calculator or software program to check your work and ensure accuracy.

In conclusion, mastering graphing from factored form requires practice and patience, but with the right strategies and tools, anyone can become proficient. By using the methods outlined in this article, you can improve your skills and become more confident in your ability to graph quadratic equations.

What do you think? Have you ever struggled with graphing from factored form? Share your experiences and tips in the comments below!