Mastering graphing equations in standard form is a fundamental skill in mathematics, particularly in algebra and geometry. Graphing equations helps visualize the relationship between variables, making it easier to understand and analyze the behavior of functions. In this article, we will explore five ways to master graphing equations in standard form, providing you with practical tips and techniques to improve your skills.
Understanding Standard Form

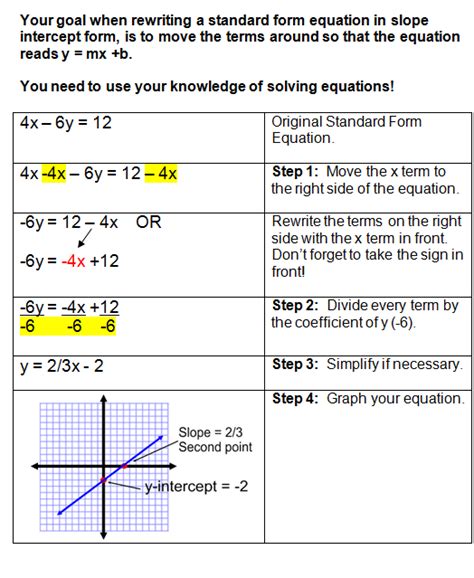
Before diving into graphing equations, it's essential to understand what standard form means. In mathematics, standard form refers to a specific way of writing equations, typically in the form of Ax + By = C, where A, B, and C are constants. This form is also known as the general form or the slope-intercept form. Understanding the concept of standard form is crucial for graphing equations, as it helps you identify the slope, y-intercept, and x-intercept of a line.
Method 1: Using the Slope-Intercept Method

The slope-intercept method is a popular technique for graphing equations in standard form. This method involves identifying the slope (m) and the y-intercept (b) from the equation, and then using these values to plot the line on a graph. To use the slope-intercept method, follow these steps:
- Identify the slope (m) by looking at the coefficient of x in the equation.
- Identify the y-intercept (b) by looking at the constant term in the equation.
- Plot the y-intercept on the graph.
- Use the slope to plot additional points on the graph.
For example, consider the equation 2x + 3y = 6. Using the slope-intercept method, we can identify the slope (m = -2/3) and the y-intercept (b = 2). Plotting the y-intercept and using the slope, we can graph the equation.
Method 2: Using the Table of Values Method

The table of values method is another effective way to graph equations in standard form. This method involves creating a table of values by substituting different x-values into the equation and calculating the corresponding y-values. To use the table of values method, follow these steps:
- Create a table with x-values and corresponding y-values.
- Substitute different x-values into the equation and calculate the corresponding y-values.
- Plot the points on the graph.
- Draw a line through the points to graph the equation.
For example, consider the equation x - 2y = 4. Using the table of values method, we can create a table of values with x-values and corresponding y-values. Plotting the points and drawing a line through them, we can graph the equation.
Benefits of the Table of Values Method
The table of values method has several benefits, including:
- It allows you to visualize the relationship between x and y values.
- It helps you identify patterns and trends in the data.
- It is a useful method for graphing non-linear equations.
Method 3: Using the Graphing Calculator Method

The graphing calculator method is a modern approach to graphing equations in standard form. This method involves using a graphing calculator to visualize the graph of the equation. To use the graphing calculator method, follow these steps:
- Enter the equation into the graphing calculator.
- Set the x-axis and y-axis scales.
- Graph the equation using the calculator.
- Analyze the graph to identify key features, such as the slope, y-intercept, and x-intercept.
For example, consider the equation 3x - 2y = 5. Using a graphing calculator, we can enter the equation and graph it. Analyzing the graph, we can identify the slope, y-intercept, and x-intercept.
Method 4: Using the Point-Slope Form Method

The point-slope form method is another technique for graphing equations in standard form. This method involves converting the equation to point-slope form, which is in the form of y - y1 = m(x - x1). To use the point-slope form method, follow these steps:
- Convert the equation to point-slope form.
- Identify the slope (m) and the point (x1, y1).
- Plot the point on the graph.
- Use the slope to plot additional points on the graph.
For example, consider the equation 2x + 3y = 6. Converting the equation to point-slope form, we get y - 2 = (-2/3)(x - 0). Plotting the point and using the slope, we can graph the equation.
Method 5: Using the X-Intercept and Y-Intercept Method

The x-intercept and y-intercept method is a simple and effective way to graph equations in standard form. This method involves identifying the x-intercept and y-intercept from the equation, and then plotting these points on the graph. To use the x-intercept and y-intercept method, follow these steps:
- Identify the x-intercept by setting y = 0 and solving for x.
- Identify the y-intercept by setting x = 0 and solving for y.
- Plot the x-intercept and y-intercept on the graph.
- Draw a line through the points to graph the equation.
For example, consider the equation x - 2y = 4. Identifying the x-intercept and y-intercept, we can plot these points on the graph and draw a line through them to graph the equation.
What is standard form in mathematics?
+Standard form in mathematics refers to a specific way of writing equations, typically in the form of Ax + By = C, where A, B, and C are constants.
What is the slope-intercept method?
+The slope-intercept method is a technique for graphing equations in standard form, involving identifying the slope (m) and the y-intercept (b) from the equation, and then using these values to plot the line on a graph.
What is the point-slope form method?
+The point-slope form method is a technique for graphing equations in standard form, involving converting the equation to point-slope form, which is in the form of y - y1 = m(x - x1).
We hope this article has provided you with a comprehensive understanding of graphing equations in standard form. By mastering these five methods, you will be able to tackle a wide range of graphing problems with confidence. Remember to practice regularly and apply these techniques to different types of equations. With persistence and dedication, you will become proficient in graphing equations in standard form.