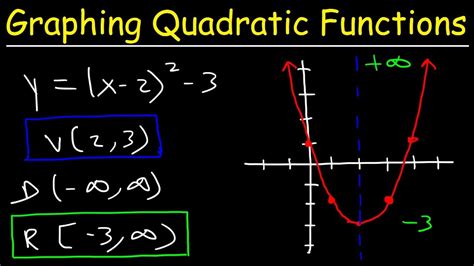
Graphing quadratics in vertex form is a fundamental concept in algebra and mathematics. The vertex form of a quadratic function is written as f(x) = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola. Understanding how to graph quadratics in vertex form can help you visualize and analyze the behavior of quadratic functions.
Why Graph Quadratics in Vertex Form?

Graphing quadratics in vertex form can be beneficial in various ways. Firstly, it allows you to easily identify the vertex, axis of symmetry, and the direction of the parabola's opening. This information can be crucial in solving problems related to quadratic functions, such as finding the maximum or minimum values of the function.
Identifying the Vertex and Axis of Symmetry
In the vertex form of a quadratic function, the vertex is represented by the point (h, k). The axis of symmetry is a vertical line that passes through the vertex and is perpendicular to the x-axis. To graph a quadratic in vertex form, start by plotting the vertex on the coordinate plane.
Method 1: Plotting the Vertex and Axis of Symmetry

To plot the vertex and axis of symmetry, follow these steps:
- Identify the values of h and k from the vertex form of the quadratic function.
- Plot the point (h, k) on the coordinate plane.
- Draw a vertical line through the vertex to represent the axis of symmetry.
Plotting Additional Points
After plotting the vertex and axis of symmetry, you can plot additional points to complete the graph of the quadratic function. To do this, substitute x-values into the equation and calculate the corresponding y-values.
Method 2: Plotting Additional Points

To plot additional points, follow these steps:
- Choose x-values on either side of the axis of symmetry.
- Substitute the x-values into the equation and calculate the corresponding y-values.
- Plot the points on the coordinate plane.
Using a Table of Values
Another way to graph a quadratic in vertex form is to use a table of values. This method involves creating a table with x-values and corresponding y-values.
Method 3: Using a Table of Values

To use a table of values, follow these steps:
- Create a table with x-values and corresponding y-values.
- Plot the points on the coordinate plane.
- Draw a smooth curve through the points to complete the graph.
Graphing Quadratics with a Vertical Stretch or Compression
When graphing quadratics in vertex form, you may encounter functions with a vertical stretch or compression. A vertical stretch or compression occurs when the coefficient of the squared term is not equal to 1.
Method 4: Graphing Quadratics with a Vertical Stretch or Compression

To graph a quadratic with a vertical stretch or compression, follow these steps:
- Identify the coefficient of the squared term.
- Determine the direction of the stretch or compression.
- Plot the vertex and axis of symmetry.
- Plot additional points, taking into account the stretch or compression.
Graphing Quadratics with a Horizontal Shift
Finally, you may encounter quadratics in vertex form with a horizontal shift. A horizontal shift occurs when the x-term is not equal to 0.
Method 5: Graphing Quadratics with a Horizontal Shift

To graph a quadratic with a horizontal shift, follow these steps:
- Identify the x-term.
- Determine the direction of the shift.
- Plot the vertex and axis of symmetry.
- Plot additional points, taking into account the shift.
In conclusion, graphing quadratics in vertex form can be achieved using various methods. By understanding how to plot the vertex, axis of symmetry, and additional points, you can effectively graph quadratic functions and analyze their behavior.
What is the vertex form of a quadratic function?
+The vertex form of a quadratic function is written as f(x) = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola.
How do I identify the vertex and axis of symmetry of a quadratic function in vertex form?
+Identify the values of h and k from the vertex form of the quadratic function. The vertex is represented by the point (h, k), and the axis of symmetry is a vertical line that passes through the vertex and is perpendicular to the x-axis.
How do I plot additional points to complete the graph of a quadratic function in vertex form?
+Choose x-values on either side of the axis of symmetry, substitute the x-values into the equation, and calculate the corresponding y-values. Plot the points on the coordinate plane.