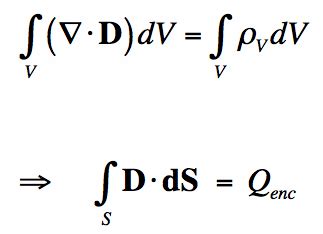Gauss Law In Integral Form Explained Simply

Quick Links :

Gauss's law is a fundamental concept in physics, particularly in the field of electromagnetism. It helps us understand the relationship between electric charges and the resulting electric fields. While Gauss's law can be expressed in both differential and integral forms, we'll focus on the integral form in this article. By the end of this explanation, you'll have a clear understanding of Gauss's law in integral form and its significance in physics.

What is Gauss's Law?

Gauss's law, also known as Gauss's flux theorem, is a mathematical statement that describes the distribution of electric charge in relation to the resulting electric field. It was formulated by Carl Friedrich Gauss in the 19th century and has since become a cornerstone of electromagnetism. Gauss's law is often used to calculate the electric field around charged objects, such as spheres, cylinders, and planes.

Electric Flux and Gauss's Law

To understand Gauss's law, we need to define electric flux. Electric flux is a measure of the amount of electric field that passes through a given surface. It's a way to quantify the "flow" of electric field lines through a surface. Gauss's law states that the total electric flux through a closed surface is proportional to the charge enclosed within that surface.

Gauss's Law in Integral Form

Gauss's law in integral form is expressed mathematically as:

Φ = Q / ε₀

where Φ is the electric flux, Q is the charge enclosed, and ε₀ is the electric constant (also known as the permittivity of free space).

This equation states that the electric flux through a closed surface is equal to the charge enclosed divided by the electric constant.

Surface Integral and Gauss's Law

The surface integral is a crucial part of Gauss's law in integral form. It's used to calculate the electric flux through a surface. The surface integral is defined as:

Φ = ∮ E · dA

where E is the electric field, dA is the surface area element, and ∮ denotes the surface integral.

How to Apply Gauss's Law in Integral Form

Applying Gauss's law in integral form involves several steps:

1. Define the surface: Identify the surface through which you want to calculate the electric flux. This surface is usually a closed surface, such as a sphere or a cube.
2. Determine the charge enclosed: Find the total charge enclosed within the surface. This charge can be a point charge, a line charge, or a surface charge.
3. Calculate the electric field: Determine the electric field at each point on the surface. You can use Coulomb's law or other methods to calculate the electric field.
4. Evaluate the surface integral: Calculate the surface integral using the electric field and surface area element.

Examples of Gauss's Law in Integral Form

Here are a few examples of applying Gauss's law in integral form:

• A point charge: A point charge is enclosed within a spherical surface. The electric flux through the surface is equal to the charge divided by the electric constant.
• A line charge: A line charge is enclosed within a cylindrical surface. The electric flux through the surface is equal to the charge per unit length divided by the electric constant.
• A surface charge: A surface charge is enclosed within a flat surface. The electric flux through the surface is equal to the surface charge density divided by the electric constant.

Benefits of Gauss's Law in Integral Form

Gauss's law in integral form has several benefits:

• Simplifies calculations: Gauss's law can simplify calculations involving electric fields and charges.
• Provides insight: Gauss's law provides insight into the relationship between electric charges and the resulting electric fields.
• Applies to complex systems: Gauss's law can be applied to complex systems, such as those involving multiple charges and surfaces.

Common Misconceptions about Gauss's Law

There are several common misconceptions about Gauss's law:

• Gauss's law only applies to simple systems: Gauss's law can be applied to complex systems involving multiple charges and surfaces.
• Gauss's law is only used for electric fields: Gauss's law can be used for magnetic fields as well.
• Gauss's law is a difficult concept: Gauss's law is a fundamental concept in physics, but it can be challenging to apply.

Real-World Applications of Gauss's Law

Gauss's law has several real-world applications:

• Electrostatics: Gauss's law is used to calculate the electric field around charged objects, such as capacitors and resistors.
• Electromagnetics: Gauss's law is used to calculate the magnetic field around currents and charges.
• Engineering: Gauss's law is used in the design of electronic devices, such as antennas and filters.

Conclusion

Gauss's law in integral form is a powerful tool for understanding the relationship between electric charges and the resulting electric fields. By applying Gauss's law, you can simplify calculations, gain insight into complex systems, and design electronic devices. Remember to define the surface, determine the charge enclosed, calculate the electric field, and evaluate the surface integral when applying Gauss's law.

We hope this explanation has helped you understand Gauss's law in integral form. If you have any questions or comments, please share them below.