Convert Quadratic To Vertex Form Calculator Online Tool

Quick Links :

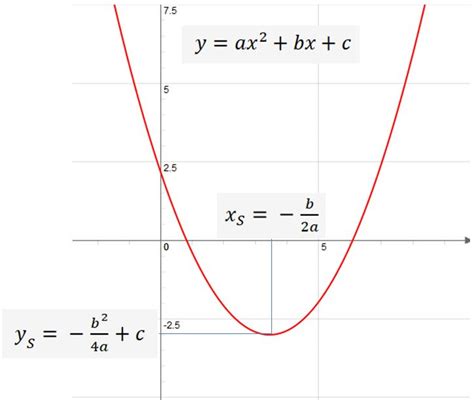
Converting quadratic equations to vertex form is a crucial skill in algebra and mathematics. A quadratic equation in standard form is represented as ax^2 + bx + c, where a, b, and c are constants. However, this form doesn't immediately reveal key information about the parabola it represents, such as the vertex. The vertex form of a quadratic equation, on the other hand, is represented as a(x - h)^2 + k, where (h, k) is the vertex of the parabola.

This article explores the process of converting quadratic equations to vertex form using an online calculator tool, discussing the importance of this conversion, the steps involved, and how it enhances our understanding of quadratic functions.

Understanding Quadratic Equations

Quadratic equations are polynomial equations of degree two, meaning the highest power of the variable (usually x) is two. These equations are fundamental in mathematics and appear in various areas, including physics, engineering, economics, and computer science. Quadratic equations can be used to model real-world phenomena, such as the trajectory of projectiles, the shape of mirrors and lenses, and the design of electronic circuits.

The Standard Form of Quadratic Equations

The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0. This form is useful for solving quadratic equations using various methods, such as factoring, the quadratic formula, and completing the square. However, it doesn't provide immediate information about the vertex of the parabola.

The Importance of Vertex Form

The vertex form of a quadratic equation, a(x - h)^2 + k, provides valuable information about the parabola it represents. The vertex (h, k) is the minimum or maximum point of the parabola, depending on the sign of the coefficient a. This information is crucial in various applications, such as finding the maximum height of a projectile, the minimum cost of production, or the maximum revenue of a business.

Converting Quadratic Equations to Vertex Form

Converting a quadratic equation from standard form to vertex form involves a process called completing the square. This process involves manipulating the equation to create a perfect square trinomial, which can be factored into the square of a binomial.

Steps to Convert Quadratic Equations to Vertex Form

1. Start with the standard form: Begin with the quadratic equation in standard form, ax^2 + bx + c.
2. Move the constant term: Move the constant term c to the right-hand side of the equation.
3. Group the x terms: Group the x terms on the left-hand side of the equation.
4. Complete the square: Add and subtract (b/2)^2 to the left-hand side of the equation to create a perfect square trinomial.
5. Factor the trinomial: Factor the perfect square trinomial into the square of a binomial.
6. Write in vertex form: Write the equation in vertex form, a(x - h)^2 + k.

Using an Online Calculator Tool

Converting quadratic equations to vertex form can be a time-consuming and error-prone process. Fortunately, online calculator tools are available to simplify this process. These tools can convert quadratic equations to vertex form instantly, providing the vertex coordinates and the equation in vertex form.

Benefits of Using an Online Calculator Tool

• Saves time: Online calculator tools can convert quadratic equations to vertex form quickly, saving time and effort.
• Reduces errors: These tools can reduce errors associated with completing the square, ensuring accurate results.
• Provides insight: Online calculator tools can provide insight into the vertex form of quadratic equations, enhancing our understanding of quadratic functions.

Conclusion

Converting quadratic equations to vertex form is a crucial skill in algebra and mathematics. The vertex form provides valuable information about the parabola, including the vertex coordinates. Online calculator tools can simplify this process, saving time and reducing errors. By using these tools, we can enhance our understanding of quadratic functions and apply them to real-world problems.

Take Action

Try converting a quadratic equation to vertex form using an online calculator tool. Experiment with different equations and explore the benefits of using these tools. Share your experiences and insights with others, and explore how quadratic functions can be applied to real-world problems.