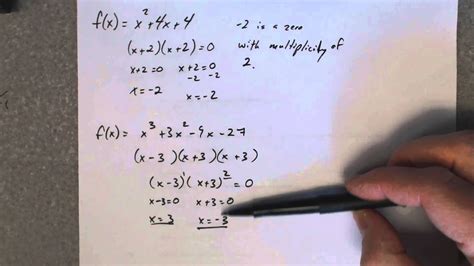Form Polynomial With Given Zeros And Degree Calculator Tool

Quick Links :

Polynomials are fundamental concepts in mathematics, and understanding how to form them with given zeros and degree is crucial for various applications in algebra, calculus, and other branches of mathematics. In this article, we will delve into the concept of polynomials, explore how to form them with given zeros and degree, and discuss the calculator tool that simplifies this process.

Understanding Polynomials

A polynomial is an expression consisting of variables and coefficients combined using only addition, subtraction, and multiplication. It can be written in the general form of:

P(x) = a_nx^n + a_(n-1)x^(n-1) +... + a_1x + a_0

where a_n, a_(n-1),..., a_1, a_0 are constants, and x is the variable. The degree of a polynomial is the highest power of the variable, which in this case is n.

Forming Polynomials with Given Zeros

Given the zeros of a polynomial, we can form the polynomial using the factored form. If p(x) has zeros at x = r_1, r_2,..., r_n, then it can be written as:

p(x) = a(x - r_1)(x - r_2)...(x - r_n)

where a is a constant. This form is useful for finding the polynomial given its zeros.

Steps to Form a Polynomial with Given Zeros

1. List the zeros of the polynomial.
2. Write the factored form of the polynomial using the zeros.
3. Multiply the factors to obtain the expanded form of the polynomial.

Example: Given the zeros x = 1, 2, and 3, form the polynomial.

Solution:

p(x) = a(x - 1)(x - 2)(x - 3) p(x) = a(x^2 - 3x + 2)(x - 3) p(x) = a(x^3 - 6x^2 + 11x - 6)

Forming Polynomials with Given Degree and Zeros

When given the degree and zeros of a polynomial, we can form the polynomial using the factored form and the degree. If p(x) has degree n and zeros at x = r_1, r_2,..., r_n, then it can be written as:

p(x) = a(x - r_1)(x - r_2)...(x - r_n)

where a is a constant.

Steps to Form a Polynomial with Given Degree and Zeros

1. List the zeros of the polynomial.
2. Write the factored form of the polynomial using the zeros and degree.
3. Multiply the factors to obtain the expanded form of the polynomial.

Example: Given the degree 3 and zeros x = 1, 2, form the polynomial.

Solution:

p(x) = a(x - 1)(x - 2)(x - r) p(x) = a(x^2 - 3x + 2)(x - r)

To find the value of r, we can use the fact that the degree of the polynomial is 3.

p(x) = a(x^3 - 6x^2 + 11x - 6)

Polynomial Calculator Tool

The polynomial calculator tool is an online calculator that simplifies the process of forming polynomials with given zeros and degree. This tool allows users to input the zeros and degree of the polynomial and generates the factored and expanded forms of the polynomial.

Benefits of the Polynomial Calculator Tool

1. Simplifies the process of forming polynomials with given zeros and degree.
2. Saves time and effort in calculations.
3. Provides accurate results.
4. Allows users to visualize the polynomial in factored and expanded forms.

Conclusion and Next Steps

In this article, we explored the concept of polynomials, how to form them with given zeros and degree, and discussed the polynomial calculator tool that simplifies this process. By understanding how to form polynomials, you can apply this knowledge to various mathematical concepts, such as solving equations and finding roots.

We invite you to try out the polynomial calculator tool and explore its features. Share your experiences and feedback with us in the comments section below. If you have any questions or need further clarification on any of the topics discussed, please don't hesitate to ask.