4 Ways To Find X-Intercepts In Unfactored Form

Quick Links :

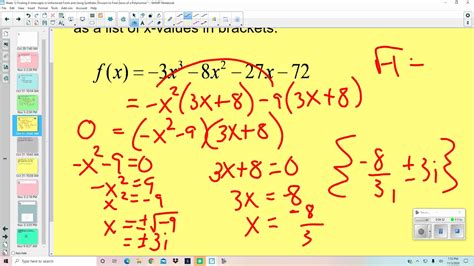
Finding the x-intercepts of a quadratic equation is a fundamental concept in algebra, and it's essential to understand the different methods to achieve this. In this article, we'll explore four ways to find x-intercepts in unfactored form, which is a quadratic equation that cannot be easily factored into the product of two binomials.

Understanding X-Intercepts

Before we dive into the methods, let's briefly discuss what x-intercepts represent. The x-intercept of a quadratic equation is the point where the graph of the equation crosses the x-axis. In other words, it's the value of x that makes the equation equal to zero.

Method 1: Factoring (When Possible)

While we're focusing on unfactored form, it's essential to acknowledge that factoring is still a viable method when the quadratic equation can be factored into the product of two binomials. If the equation can be factored, it's often the simplest way to find the x-intercepts.

For example, consider the quadratic equation:

x^2 + 5x + 6 = 0

This equation can be factored as:

(x + 3)(x + 2) = 0

By setting each factor equal to zero, we find the x-intercepts:

x + 3 = 0 --> x = -3 x + 2 = 0 --> x = -2

However, not all quadratic equations can be factored, which is where the next three methods come in.

Method 2: Quadratic Formula

The quadratic formula is a powerful tool for finding x-intercepts, especially when the equation cannot be factored. The quadratic formula is:

x = (-b ± √(b^2 - 4ac)) / 2a

where a, b, and c are the coefficients of the quadratic equation.

For example, consider the quadratic equation:

x^2 + 4x + 5 = 0

Using the quadratic formula, we get:

x = (-(4) ± √((4)^2 - 4(1)(5))) / 2(1) x = (-4 ± √(16 - 20)) / 2 x = (-4 ± √(-4)) / 2

Simplifying further, we find the x-intercepts:

x = (-4 ± 2i) / 2 x = -2 ± i

Method 3: Graphing

Graphing is a visual approach to finding x-intercepts. By plotting the quadratic equation on a graph, you can identify the points where the graph crosses the x-axis.

For example, consider the quadratic equation:

x^2 - 3x - 4 = 0

Graphing the equation, we find the x-intercepts:

x ≈ -1.3 and x ≈ 3.3

Note that graphing may not provide exact values, but it can give you an approximate idea of the x-intercepts.

Method 4: Completing the Square

Completing the square is a method that involves manipulating the quadratic equation to create a perfect square trinomial. This method can be used to find x-intercepts, especially when the equation is in the form ax^2 + bx + c = 0.

For example, consider the quadratic equation:

x^2 + 6x + 8 = 0

Completing the square, we get:

x^2 + 6x + 9 - 1 = 0 (x + 3)^2 - 1 = 0

Rearranging, we find the x-intercepts:

(x + 3)^2 = 1 x + 3 = ±1 x = -3 ± 1 x = -4 and x = -2

In conclusion, finding x-intercepts in unfactored form requires different methods, each with its strengths and weaknesses. By understanding these methods, you can approach quadratic equations with confidence and find the x-intercepts with ease.

Take Action!

Now that you've learned four ways to find x-intercepts in unfactored form, try practicing with different quadratic equations. Remember to use the quadratic formula, graphing, and completing the square methods to find the x-intercepts.

Share your experiences and questions in the comments below, and don't forget to share this article with your friends and classmates who may benefit from it!