Vertex Form Calculator: Easy Quadratic Equation Solutions

Quick Links :

Quadratic equations are a fundamental part of algebra, and solving them can be a daunting task for many students. However, with the right tools and techniques, it can be made much easier. One such technique is using the vertex form of a quadratic equation, which can simplify the process of finding the solutions. In this article, we will explore the concept of vertex form and how to use a vertex form calculator to easily solve quadratic equations.

Quadratic equations are polynomial equations of degree two, which means the highest power of the variable (usually x) is two. The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants. However, this form can be difficult to work with, especially when trying to find the solutions. This is where the vertex form comes in.

What is Vertex Form?

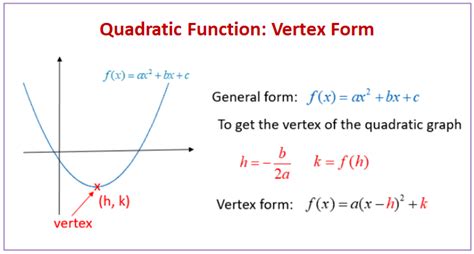
The vertex form of a quadratic equation is a way of expressing the equation in a more convenient form, which makes it easier to find the solutions. The vertex form is given by:

y = a(x - h)^2 + k

where (h, k) is the vertex of the parabola. The vertex is the lowest or highest point on the parabola, depending on whether the parabola opens upwards or downwards.

Benefits of Using Vertex Form

There are several benefits to using the vertex form of a quadratic equation. One of the main advantages is that it makes it easy to find the vertex of the parabola, which is essential for finding the solutions. Additionally, the vertex form can be used to determine the axis of symmetry, which is the vertical line that passes through the vertex.

How to Use a Vertex Form Calculator

Using a vertex form calculator is a straightforward process. Simply enter the values of a, b, and c from the standard form of the quadratic equation, and the calculator will convert it to vertex form. Some calculators may also provide additional information, such as the vertex and axis of symmetry.

Step-by-Step Guide to Using a Vertex Form Calculator

Here is a step-by-step guide to using a vertex form calculator:

1. Enter the values of a, b, and c from the standard form of the quadratic equation.
2. Choose the correct form of the equation (e.g., ax^2 + bx + c = 0).
3. Click the "Calculate" button to convert the equation to vertex form.
4. The calculator will display the vertex form of the equation, along with the vertex and axis of symmetry.

Practical Examples of Using a Vertex Form Calculator

Here are a few practical examples of using a vertex form calculator:

Example 1: Find the vertex form of the equation x^2 + 5x + 6 = 0.

Using a vertex form calculator, we get:

y = (x + 2.5)^2 - 6.25

The vertex is (-2.5, -6.25), and the axis of symmetry is x = -2.5.

Example 2: Find the vertex form of the equation 2x^2 - 3x - 1 = 0.

Using a vertex form calculator, we get:

y = 2(x - 0.75)^2 - 1.5

The vertex is (0.75, -1.5), and the axis of symmetry is x = 0.75.

Common Mistakes to Avoid When Using a Vertex Form Calculator

Here are a few common mistakes to avoid when using a vertex form calculator:

1. Entering the wrong values for a, b, and c.
2. Choosing the wrong form of the equation.
3. Not checking the units of the input values.

By avoiding these common mistakes, you can ensure that you get accurate results from your vertex form calculator.

Conclusion and Final Thoughts

In conclusion, using a vertex form calculator is a powerful tool for solving quadratic equations. By converting the equation to vertex form, you can easily find the vertex and axis of symmetry, which makes it much easier to find the solutions. Whether you're a student or a professional, a vertex form calculator is an essential tool to have in your toolkit.

So, next time you're faced with a quadratic equation, don't be afraid to use a vertex form calculator. With its help, you'll be able to solve the equation with ease and accuracy.