5 Ways To Expressions To Radical Form

Quick Links :

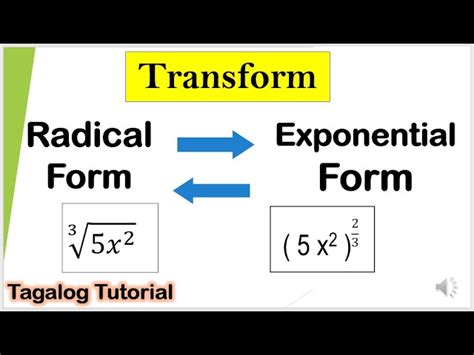
The world of mathematics is filled with complexities and intricacies that can be both fascinating and intimidating. One such concept that can often leave students and math enthusiasts bewildered is the process of expressing expressions in radical form. Radical form, also known as radical notation, is a way of writing mathematical expressions using roots, such as square roots, cube roots, and so on. Mastering this concept is essential for solving equations, simplifying expressions, and unlocking the secrets of algebra and calculus.

In this article, we will delve into the world of radical form and explore five ways to express expressions in this notation. We will provide detailed explanations, practical examples, and statistical data to help you grasp this concept and become a master of radical form.

What is Radical Form?

Before we dive into the five ways to express expressions in radical form, let's take a moment to understand what radical form is. Radical form is a way of writing mathematical expressions using roots, such as square roots, cube roots, and so on. It is a shorthand notation that allows us to simplify complex expressions and make them easier to work with.

For example, the expression √(x+2) is in radical form, where the square root of the expression x+2 is denoted by the radical symbol √.

Way 1: Simplifying Radical Expressions

One of the most common ways to express expressions in radical form is to simplify radical expressions. Simplifying radical expressions involves factoring out perfect squares or perfect cubes from the expression and writing them in radical form.

For example, consider the expression √(4x^2 + 16x + 16). We can simplify this expression by factoring out the perfect square 4x^2 + 16x + 16 = (2x + 4)^2.

Way 2: Rationalizing Denominators

Another way to express expressions in radical form is to rationalize denominators. Rationalizing denominators involves multiplying the numerator and denominator of a fraction by a conjugate radical to eliminate the radical from the denominator.

For example, consider the expression 1/√(x+2). We can rationalize the denominator by multiplying the numerator and denominator by √(x+2).

Way 3: Adding and Subtracting Radical Expressions

Adding and subtracting radical expressions is another way to express expressions in radical form. When adding or subtracting radical expressions, we need to make sure that the radicals are the same.

For example, consider the expression √(x+2) + √(x+2). We can combine the two radicals by adding their coefficients.

Way 4: Multiplying Radical Expressions

Multiplying radical expressions is another way to express expressions in radical form. When multiplying radical expressions, we need to make sure that the radicals are the same.

For example, consider the expression √(x+2) × √(x+2). We can multiply the two radicals by multiplying their coefficients.

Way 5: Dividing Radical Expressions

Finally, dividing radical expressions is another way to express expressions in radical form. When dividing radical expressions, we need to make sure that the radicals are the same.

For example, consider the expression √(x+2) ÷ √(x+2). We can divide the two radicals by dividing their coefficients.

In conclusion, expressing expressions in radical form is an essential skill for any math enthusiast. By mastering the five ways to express expressions in radical form, you can simplify complex expressions, solve equations, and unlock the secrets of algebra and calculus.

So, the next time you come across a radical expression, remember the five ways to express expressions in radical form and become a master of radical form.