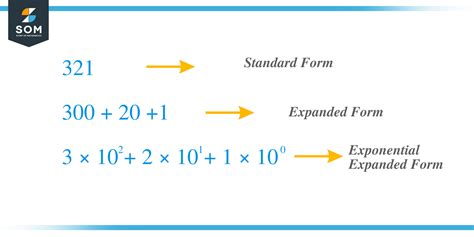
Exponents In Expanded Form Made Easy

Quick Links :

Exponents in expanded form can seem daunting at first, but with a clear understanding of the concept and practice, it can become second nature. In this article, we will delve into the world of exponents, explore what they are, and learn how to expand them with ease.

Exponents are shorthand notation for repeated multiplication of a number by itself. For instance, instead of writing 4 × 4 × 4 × 4, we can simply write 4^4. This notation is used extensively in mathematics, physics, and engineering, and is a fundamental concept in algebra. Understanding exponents is crucial for solving equations, manipulating expressions, and modeling real-world phenomena.

What are Exponents?

Exponents are a mathematical operation that represents repeated multiplication of a number by itself. The number being multiplied is called the base, and the number of times it is multiplied is called the exponent. For example, in the expression 2^3, the base is 2 and the exponent is 3. This means that 2 is multiplied by itself 3 times, resulting in 2 × 2 × 2 = 8.

Why are Exponents Important?

Exponents play a vital role in various mathematical concepts, such as algebra, geometry, and calculus. They help simplify complex expressions, making it easier to solve equations and manipulate formulas. Exponents are also used to model real-world phenomena, such as population growth, chemical reactions, and physical laws.

Expanded Form of Exponents

The expanded form of an exponent is the process of writing the repeated multiplication of the base by itself. For example, the expanded form of 2^3 is 2 × 2 × 2. This can be written as:

2^3 = 2 × 2 × 2 = 8

Similarly, the expanded form of 3^4 is:

3^4 = 3 × 3 × 3 × 3 = 81

Rules for Expanding Exponents

There are several rules to keep in mind when expanding exponents:

• The base is multiplied by itself as many times as the exponent indicates.
• The exponent is written as a superscript, which means it is written above the base.
• When multiplying two numbers with the same base, the exponents are added. For example, 2^2 × 2^3 = 2^(2+3) = 2^5.
• When dividing two numbers with the same base, the exponents are subtracted. For example, 2^5 ÷ 2^3 = 2^(5-3) = 2^2.

Examples of Expanding Exponents

Here are some examples of expanding exponents:

• 2^4 = 2 × 2 × 2 × 2 = 16
• 3^2 = 3 × 3 = 9
• 4^3 = 4 × 4 × 4 = 64
• 5^1 = 5 (since any number raised to the power of 1 is the number itself)

Real-World Applications of Expanding Exponents

Expanding exponents has numerous real-world applications in fields such as:

• Physics: Exponents are used to describe the laws of motion, energy, and gravity.
• Engineering: Exponents are used to design and optimize systems, such as electronic circuits and mechanical structures.
• Economics: Exponents are used to model population growth, inflation, and economic trends.
• Computer Science: Exponents are used in algorithms and data structures, such as binary search and sorting.

Conclusion: Mastering Exponents in Expanded Form

Mastering exponents in expanded form is a fundamental skill that requires practice and patience. By understanding the concept of exponents, rules for expanding them, and real-world applications, you can become proficient in manipulating expressions and solving equations. Remember to practice regularly and apply your knowledge to real-world problems to reinforce your understanding of exponents.

We hope this article has helped you understand exponents in expanded form and how to apply them in various contexts. If you have any questions or comments, please share them below.