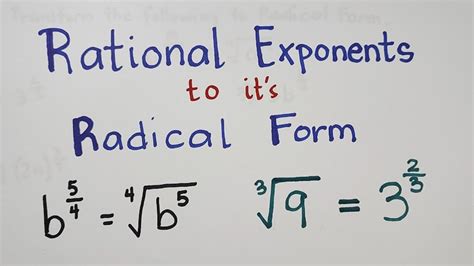Understanding Exponential and Radical Forms

Exponential and radical forms are two different ways to express the same mathematical value. Exponential form represents a number as a power of another number, while radical form represents a number as the root of another number. Understanding the relationship between these two forms is crucial for solving mathematical problems and manipulating equations.
Why Convert Exponential to Radical Form?
Converting exponential form to radical form can be useful in various mathematical contexts. For instance, it can help simplify complex equations, make calculations easier, and provide a more intuitive understanding of mathematical relationships. In this article, we will explore five ways to convert exponential form to radical form.
Method 1: Using the Definition of Exponents

One way to convert exponential form to radical form is by using the definition of exponents. The definition states that a^(1/n) = nth root of a. Using this definition, we can convert exponential form to radical form by changing the exponent to a root.
Example:
- 2^(1/3) = 3rd root of 2 = ∛2
How it Works
To convert exponential form to radical form using this method, follow these steps:
- Identify the base and exponent in the exponential expression.
- Change the exponent to a root by dividing 1 by the exponent.
- Write the base as the radicand (the number inside the radical sign).
For example, to convert 2^(1/3) to radical form, we identify the base (2) and exponent (1/3). We then change the exponent to a root by dividing 1 by 1/3, which gives us 3. Finally, we write the base as the radicand, resulting in ∛2.
Method 2: Using Fractional Exponents

Another way to convert exponential form to radical form is by using fractional exponents. Fractional exponents are exponents that are fractions, and they can be used to represent radicals.
Example:
- 2^(1/3) = 2^0.33
How it Works
To convert exponential form to radical form using this method, follow these steps:
- Identify the base and exponent in the exponential expression.
- Convert the exponent to a decimal by dividing the numerator by the denominator.
- Write the base as the radicand, and the decimal exponent as the index (the number outside the radical sign).
For example, to convert 2^(1/3) to radical form, we identify the base (2) and exponent (1/3). We then convert the exponent to a decimal by dividing 1 by 3, which gives us 0.33. Finally, we write the base as the radicand and the decimal exponent as the index, resulting in 2^0.33.
Method 3: Using the Properties of Exponents

We can also convert exponential form to radical form using the properties of exponents. One such property is that a^(m/n) = (a^m)^(1/n).
Example:
- 2^(2/3) = (2^2)^(1/3) = 4^(1/3) = ∛4
How it Works
To convert exponential form to radical form using this method, follow these steps:
- Identify the base and exponent in the exponential expression.
- Factor the exponent into a product of two numbers, one of which is 1.
- Write the base as the radicand, and the factored exponent as the index.
For example, to convert 2^(2/3) to radical form, we identify the base (2) and exponent (2/3). We then factor the exponent into a product of two numbers, one of which is 1, resulting in (2^2)^(1/3). Finally, we write the base as the radicand and the factored exponent as the index, resulting in ∛4.
Method 4: Using the Rational Exponent Rule

The rational exponent rule states that a^m = a^(m/n) when n is an integer. We can use this rule to convert exponential form to radical form.
Example:
- 2^(1/2) = 2^1/2 = √2
How it Works
To convert exponential form to radical form using this method, follow these steps:
- Identify the base and exponent in the exponential expression.
- Rewrite the exponent as a fraction with the same numerator and denominator.
- Write the base as the radicand, and the exponent as the index.
For example, to convert 2^(1/2) to radical form, we identify the base (2) and exponent (1/2). We then rewrite the exponent as a fraction with the same numerator and denominator, resulting in 1/2. Finally, we write the base as the radicand and the exponent as the index, resulting in √2.
Method 5: Using the Radical Exponent Rule

The radical exponent rule states that a^(1/n) = nth root of a. We can use this rule to convert exponential form to radical form.
Example:
- 2^(1/3) = ∛2
How it Works
To convert exponential form to radical form using this method, follow these steps:
- Identify the base and exponent in the exponential expression.
- Rewrite the exponent as a root by dividing 1 by the exponent.
- Write the base as the radicand.
For example, to convert 2^(1/3) to radical form, we identify the base (2) and exponent (1/3). We then rewrite the exponent as a root by dividing 1 by 1/3, which gives us 3. Finally, we write the base as the radicand, resulting in ∛2.
By using these five methods, we can convert exponential form to radical form with ease. Whether we use the definition of exponents, fractional exponents, the properties of exponents, the rational exponent rule, or the radical exponent rule, we can simplify complex equations and gain a deeper understanding of mathematical relationships.
What is the difference between exponential and radical forms?
+Exponential form represents a number as a power of another number, while radical form represents a number as the root of another number.
Why is it important to convert exponential form to radical form?
+Converting exponential form to radical form can help simplify complex equations, make calculations easier, and provide a more intuitive understanding of mathematical relationships.
What are the five methods for converting exponential form to radical form?
+The five methods are: using the definition of exponents, using fractional exponents, using the properties of exponents, using the rational exponent rule, and using the radical exponent rule.
Share your thoughts and experiences with converting exponential form to radical form in the comments below!