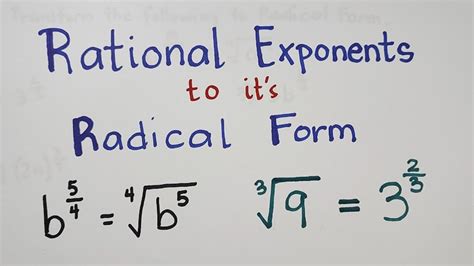5 Ways To Convert Exponential To Radical Form

Quick Links :

Converting exponential expressions to radical form is a fundamental skill in mathematics, particularly in algebra and calculus. Understanding this concept can help you simplify complex expressions, solve equations, and analyze functions. In this article, we will explore five ways to convert exponential expressions to radical form, including using properties of exponents, radical notation, and algebraic manipulations.

Understanding Exponential and Radical Forms

Before diving into the conversion methods, it's essential to understand the exponential and radical forms. An exponential expression is written in the form a^n, where a is the base and n is the exponent. On the other hand, a radical expression is written in the form √a or a^(1/n), where a is the radicand and n is the index.

Method 1: Using Properties of Exponents

One way to convert exponential expressions to radical form is by using the properties of exponents. Specifically, you can use the property a^(m/n) = (a^m)^(1/n) to rewrite the expression in radical form. For example:

• 2^(1/2) can be rewritten as √2
• 3^(2/3) can be rewritten as (3^2)^(1/3) or √(3^2)

Steps to Convert Using Properties of Exponents

1. Identify the base and exponent of the exponential expression.
2. Rewrite the exponent as a fraction, if it's not already in fractional form.
3. Apply the property a^(m/n) = (a^m)^(1/n) to rewrite the expression in radical form.

Method 2: Using Radical Notation

Another way to convert exponential expressions to radical form is by using radical notation. Radical notation involves writing the radicand and index in a specific format. For example:

• 2^(1/2) can be rewritten as √2
• 3^(2/3) can be rewritten as 3√3

Steps to Convert Using Radical Notation

1. Identify the base and exponent of the exponential expression.
2. Determine the index of the radical by finding the denominator of the fractional exponent.
3. Write the radicand and index in radical notation.

Method 3: Using Algebraic Manipulations

Algebraic manipulations can also be used to convert exponential expressions to radical form. This method involves manipulating the expression to isolate the radical. For example:

• 2^(1/2) can be rewritten as √(2^2) / √2
• 3^(2/3) can be rewritten as (3^2)^(1/3) or √(3^2)

Steps to Convert Using Algebraic Manipulations

1. Identify the base and exponent of the exponential expression.
2. Manipulate the expression to isolate the radical.
3. Simplify the expression to obtain the radical form.

Method 4: Using Fractional Exponents

Fractional exponents can be used to convert exponential expressions to radical form. This method involves rewriting the exponent as a fraction and then applying the property a^(m/n) = (a^m)^(1/n). For example:

• 2^(1/2) can be rewritten as (2^1)^(1/2)
• 3^(2/3) can be rewritten as (3^2)^(1/3)

Steps to Convert Using Fractional Exponents

1. Identify the base and exponent of the exponential expression.
2. Rewrite the exponent as a fraction, if it's not already in fractional form.
3. Apply the property a^(m/n) = (a^m)^(1/n) to rewrite the expression in radical form.

Method 5: Using Radical Equations

Radical equations can also be used to convert exponential expressions to radical form. This method involves setting up an equation with the radical and then solving for the radical. For example:

• 2^(1/2) can be rewritten as x^2 = 2
• 3^(2/3) can be rewritten as x^3 = 3^2

Steps to Convert Using Radical Equations

1. Identify the base and exponent of the exponential expression.
2. Set up an equation with the radical and the exponent.
3. Solve for the radical to obtain the radical form.

Conclusion and Next Steps

In this article, we explored five ways to convert exponential expressions to radical form. By understanding these methods, you can simplify complex expressions, solve equations, and analyze functions. Remember to practice each method to become proficient in converting exponential expressions to radical form.