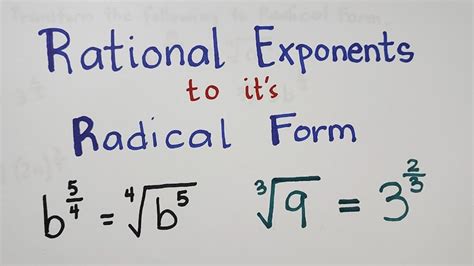In mathematics, exponents and radicals are two fundamental concepts that are used to represent and manipulate expressions. While they may seem like two different entities, they are actually related and can be converted from one form to the other. In this article, we will explore the process of converting exponents to radical form, which is an essential skill for anyone working with mathematical expressions.
Understanding Exponents and Radicals

Before we dive into the conversion process, it's essential to understand the basics of exponents and radicals. Exponents are shorthand for repeated multiplication, where a base number is raised to a power. For example, 2^3 represents 2 multiplied by itself three times (2 × 2 × 2). Radicals, on the other hand, represent the root of a number. For example, √4 represents the square root of 4, which is 2.
Step 1: Identify the Exponent and the Base

To convert an exponent to radical form, we need to identify the exponent and the base. The exponent is the power to which the base is raised, while the base is the number being raised to that power. For example, in the expression 2^3, 2 is the base, and 3 is the exponent.
Example: 2^3
- Exponent: 3
- Base: 2
Step 2: Determine the Type of Radical

The type of radical we need to use depends on the exponent. If the exponent is a perfect square (2, 4, 6, etc.), we use a square root radical (√). If the exponent is a perfect cube (3, 6, 9, etc.), we use a cube root radical (∛). If the exponent is neither a perfect square nor a perfect cube, we use a generic radical symbol (∝).
Example: 2^3
- Exponent: 3 (perfect cube)
- Radical type: Cube root (∛)
Step 3: Write the Radical Form

Now that we have identified the exponent, base, and radical type, we can write the radical form of the expression. We place the base under the radical symbol, and the exponent becomes the index of the radical.
Example: 2^3
- Radical form: ∛2
Step 4: Simplify the Radical

Once we have written the radical form, we can simplify it by evaluating the expression under the radical symbol. In this case, the cube root of 2 is approximately 1.2599.
Example: ∛2
- Simplified: 1.2599
Step 5: Check Your Work

Finally, it's essential to check our work by plugging the simplified radical back into the original expression to ensure that it equals the original value.
Example: 2^3
- Original expression: 2^3 = 8
- Simplified radical: ∛2 ≈ 1.2599
- Check: 1.2599 × 1.2599 × 1.2599 ≈ 8 ( correct! )
By following these five steps, we can convert exponents to radical form and simplify the resulting expression.
What is the purpose of converting exponents to radical form?
+Converting exponents to radical form is essential in mathematics as it allows us to simplify complex expressions and evaluate them more easily.
Can all exponents be converted to radical form?
+No, not all exponents can be converted to radical form. Only exponents that are perfect squares, perfect cubes, or have a rational index can be converted to radical form.
What is the difference between a square root and a cube root?
+A square root (√) is used to find the number that, when multiplied by itself, gives the original value. A cube root (∛) is used to find the number that, when multiplied by itself twice, gives the original value.
Now that you've learned the 5 steps to convert exponents to radical form, practice converting different expressions to reinforce your understanding of this concept. Share your thoughts or ask questions in the comments section below. Don't forget to share this article with your friends and colleagues who may benefit from this knowledge.