Sphere Equation Standard Form

Quick Links :

Spheres are a fundamental concept in mathematics, physics, and engineering, and understanding their equation is crucial for various applications. In this article, we will delve into the standard form of the sphere equation, its significance, and its applications.

The sphere equation is a mathematical representation of a sphere, which is a three-dimensional shape that is perfectly symmetrical about its center. The equation of a sphere is essential in various fields, including physics, engineering, computer science, and mathematics. It is used to describe the shape of objects, model real-world phenomena, and solve problems involving spherical coordinates.

What is the Standard Form of the Sphere Equation?

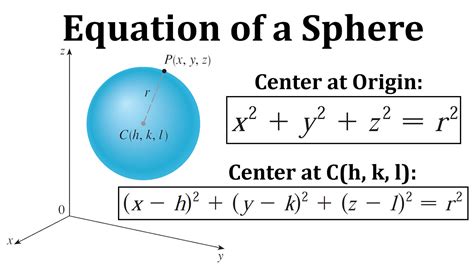
The standard form of the sphere equation is:

(x - h)^2 + (y - k)^2 + (z - l)^2 = r^2

where:

• (x, y, z) are the coordinates of a point on the sphere
• (h, k, l) are the coordinates of the center of the sphere
• r is the radius of the sphere

This equation represents a sphere with its center at (h, k, l) and a radius of r. The equation is derived from the Pythagorean theorem, which states that the square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides.

Breaking Down the Sphere Equation

The sphere equation consists of three terms, each representing the square of the distance between a point on the sphere and the center of the sphere. The first term, (x - h)^2, represents the square of the distance between the x-coordinate of the point and the x-coordinate of the center. Similarly, the second term, (y - k)^2, represents the square of the distance between the y-coordinate of the point and the y-coordinate of the center, and the third term, (z - l)^2, represents the square of the distance between the z-coordinate of the point and the z-coordinate of the center.

The sum of these three terms is equal to the square of the radius of the sphere, which represents the distance between the center of the sphere and any point on its surface.

Applications of the Sphere Equation

The sphere equation has numerous applications in various fields, including:

• Physics: The sphere equation is used to describe the shape of objects, such as balls, marbles, and planets. It is also used to model the motion of objects in three-dimensional space.
• Engineering: The sphere equation is used in computer-aided design (CAD) software to create three-dimensional models of objects. It is also used in geographic information systems (GIS) to represent the shape of the Earth.
• Computer Science: The sphere equation is used in computer graphics to create three-dimensional models of objects. It is also used in game development to create realistic simulations of objects in motion.
• Mathematics: The sphere equation is used to study the properties of spheres, such as their surface area and volume.

Real-World Examples of the Sphere Equation

• The Earth is approximately a sphere with a radius of about 6,371 kilometers. The sphere equation can be used to model the shape of the Earth and calculate its surface area and volume.
• A basketball is a sphere with a radius of about 12 centimeters. The sphere equation can be used to calculate the surface area and volume of the basketball.
• A planet is a sphere with a radius of thousands of kilometers. The sphere equation can be used to model the shape of the planet and calculate its surface area and volume.

Derivations of the Sphere Equation

The sphere equation can be derived from the Pythagorean theorem, which states that the square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides.

Let's consider a right-angled triangle with legs of length x and y, and a hypotenuse of length z. The Pythagorean theorem states that:

x^2 + y^2 = z^2

Now, let's consider a sphere with its center at the origin (0, 0, 0) and a radius of r. The equation of the sphere can be derived by considering a point on the surface of the sphere, such as (x, y, z).

Using the Pythagorean theorem, we can write:

x^2 + y^2 + z^2 = r^2

This is the equation of a sphere with its center at the origin and a radius of r.

Generalizing the Sphere Equation

The sphere equation can be generalized to represent a sphere with its center at any point (h, k, l) and a radius of r. The generalized equation is:

(x - h)^2 + (y - k)^2 + (z - l)^2 = r^2

This equation represents a sphere with its center at (h, k, l) and a radius of r.

Conclusion

In conclusion, the sphere equation is a fundamental concept in mathematics and physics, and it has numerous applications in various fields. The standard form of the sphere equation is (x - h)^2 + (y - k)^2 + (z - l)^2 = r^2, which represents a sphere with its center at (h, k, l) and a radius of r. The equation can be derived from the Pythagorean theorem and can be generalized to represent a sphere with its center at any point and a radius of r.

We hope this article has provided you with a comprehensive understanding of the sphere equation and its applications. If you have any questions or comments, please feel free to share them below.