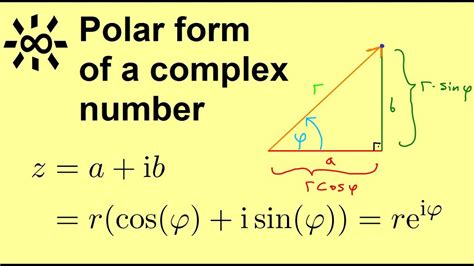Convert To Polar Form In 5 Easy Steps

Quick Links :

Converting complex numbers to polar form is a fundamental concept in mathematics and engineering, particularly in fields like electrical engineering, signal processing, and control systems. Polar form represents a complex number as a magnitude (or length) and an angle (or direction), making it easier to perform operations like multiplication and division.

What is Polar Form?

Polar form is a way to express a complex number in terms of its magnitude (r) and angle (θ). It's a two-dimensional representation that combines the real and imaginary parts of a complex number into a single magnitude and an angle. The polar form is represented as:

r(cosθ + isinθ)

where r is the magnitude (or length) and θ is the angle (or direction).

Why Convert to Polar Form?

Converting to polar form has several advantages:

• Simplifies complex number operations: Polar form makes it easier to perform operations like multiplication and division, as you can simply multiply or divide the magnitudes and add or subtract the angles.
• Provides a more intuitive representation: Polar form gives you a better understanding of the complex number's magnitude and direction, making it easier to visualize and analyze.
• Enables easier analysis of periodic signals: Polar form is particularly useful in signal processing and control systems, where periodic signals are common.

5 Easy Steps to Convert to Polar Form

Here are the 5 easy steps to convert a complex number to polar form:

Step 1: Identify the Complex Number

Start by identifying the complex number you want to convert to polar form. Let's say you have a complex number:

a + bi

where a is the real part and b is the imaginary part.

Step 2: Calculate the Magnitude

Calculate the magnitude (r) of the complex number using the formula:

r = √(a^2 + b^2)

For example, if your complex number is 3 + 4i, the magnitude would be:

r = √(3^2 + 4^2) = √(9 + 16) = √25 = 5

Step 3: Calculate the Angle

Calculate the angle (θ) of the complex number using the formula:

θ = arctan(b/a)

For example, if your complex number is 3 + 4i, the angle would be:

θ = arctan(4/3) = 53.13°

Step 4: Write the Polar Form

Write the polar form of the complex number using the magnitude and angle:

r(cosθ + isinθ)

For example, if your complex number is 3 + 4i, the polar form would be:

5(cos53.13° + isin53.13°)

Step 5: Simplify the Polar Form (Optional)

Simplify the polar form by evaluating the trigonometric functions and combining like terms.

For example, if your complex number is 3 + 4i, the simplified polar form would be:

5(0.6 + 0.8i)

Example Use Case

Suppose you're an electrical engineer designing a filter circuit. You need to convert the complex impedance of the circuit to polar form to analyze its frequency response.

The complex impedance is given as:

Z = 10 + 20i

Using the 5 steps above, you can convert the complex impedance to polar form:

r = √(10^2 + 20^2) = √(100 + 400) = √500 = 22.36

θ = arctan(20/10) = 63.43°

The polar form of the complex impedance is:

22.36(cos63.43° + isin63.43°)

Conclusion

Converting complex numbers to polar form is a simple yet powerful technique that can simplify complex number operations and provide a more intuitive representation of periodic signals. By following the 5 easy steps outlined above, you can convert any complex number to polar form and unlock the benefits of polar form representation.