3 Ways To Form A Triangle With Given Sides

Quick Links :

Hide

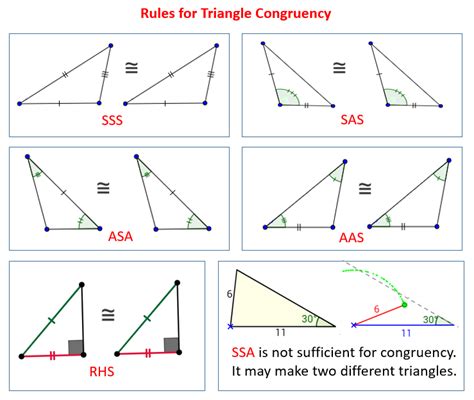
The concept of triangles is a fundamental aspect of geometry, and understanding how to form a triangle with given sides is a crucial skill in mathematics and various real-world applications. In this article, we will explore three ways to form a triangle with given sides, along with their benefits, limitations, and practical examples.

Understanding the Basics of Triangle Formation

Before diving into the methods of forming a triangle with given sides, it's essential to understand the basic conditions that must be met. The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This theorem ensures that the sides can form a valid triangle.

Method 1: Using the Law of Cosines

The Law of Cosines is a fundamental concept in trigonometry that relates the lengths of the sides of a triangle to the cosine of one of its angles. The formula is:

c² = a² + b² - 2ab * cos(C)

where c is the length of the third side, a and b are the lengths of the other two sides, and C is the angle opposite side c.

This method is useful when you know the lengths of two sides and the angle between them. By plugging in the values, you can calculate the length of the third side.

Method 2: Using the Law of Sines

The Law of Sines is another fundamental concept in trigonometry that relates the lengths of the sides of a triangle to the sines of its angles. The formula is:

a / sin(A) = b / sin(B) = c / sin(C)

where a, b, and c are the lengths of the sides, and A, B, and C are the angles opposite those sides.

This method is useful when you know the lengths of two sides and one of the angles. By plugging in the values, you can calculate the length of the third side and the other angles.

Method 3: Using Heron's Formula

Heron's Formula is a method for calculating the area of a triangle when you know the lengths of all three sides. The formula is:

Area = √(s(s-a)(s-b)(s-c))

where s is the semi-perimeter of the triangle (half the perimeter), and a, b, and c are the lengths of the sides.

This method is useful when you know the lengths of all three sides and want to calculate the area of the triangle. By plugging in the values, you can calculate the area and then use the area to calculate the length of the third side.

Benefits and Limitations of Each Method

Each method has its benefits and limitations. The Law of Cosines is useful when you know the lengths of two sides and the angle between them, but it can be complex to calculate. The Law of Sines is useful when you know the lengths of two sides and one of the angles, but it can be difficult to solve for the other angles. Heron's Formula is useful when you know the lengths of all three sides, but it can be complex to calculate the area.

In conclusion, forming a triangle with given sides requires an understanding of the basic conditions and the methods available. By using the Law of Cosines, the Law of Sines, or Heron's Formula, you can calculate the length of the third side and the other angles. Each method has its benefits and limitations, and the choice of method depends on the specific problem and the information given.

Practical Applications of Triangle Formation

The ability to form a triangle with given sides has numerous practical applications in various fields, including:

• Architecture: Triangle formation is used in building design, bridge construction, and other architectural projects.
• Engineering: Triangle formation is used in mechanical engineering, electrical engineering, and civil engineering.
• Physics: Triangle formation is used in mechanics, electromagnetism, and other areas of physics.
• Computer Science: Triangle formation is used in computer graphics, game development, and other areas of computer science.

Conclusion

Forming a triangle with given sides is a fundamental skill in mathematics and various real-world applications. By understanding the basic conditions and the methods available, you can calculate the length of the third side and the other angles. Each method has its benefits and limitations, and the choice of method depends on the specific problem and the information given. We hope this article has provided you with a comprehensive understanding of the three ways to form a triangle with given sides.

Now it's your turn! Share your thoughts and experiences with triangle formation in the comments below. Have you used any of these methods in your work or studies? Do you have any questions or need further clarification on any of the concepts discussed? Let's discuss!