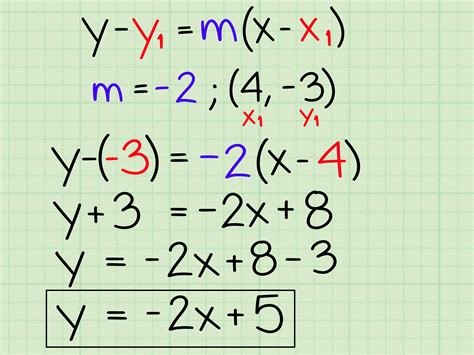Converting To Slope Intercept Form Made Easy

Quick Links :

Understanding the intricacies of slope-intercept form is crucial for mastering algebra and graphing. Slope-intercept form, denoted as y = mx + b, is a fundamental concept in mathematics that allows us to describe and analyze linear equations with ease. In this comprehensive guide, we will delve into the world of slope-intercept form, exploring its importance, benefits, and providing a step-by-step approach to converting linear equations into this versatile form.

The importance of slope-intercept form lies in its ability to simplify complex linear equations, making it easier to identify the slope and y-intercept of a line. This, in turn, enables us to graph lines with precision and analyze their behavior. Whether you're a student, teacher, or math enthusiast, grasping slope-intercept form is essential for advancing your mathematical skills.

What is Slope-Intercept Form?

Slope-intercept form is a linear equation written in the format y = mx + b, where:

• m represents the slope of the line
• b represents the y-intercept (the point where the line crosses the y-axis)
• x is the independent variable
• y is the dependent variable

This format allows us to easily identify the slope and y-intercept of a line, making it a powerful tool for graphing and analysis.

Benefits of Slope-Intercept Form

Converting linear equations to slope-intercept form offers several benefits, including:

• Simplifies complex equations: Slope-intercept form reduces linear equations to a simple and intuitive format, making it easier to understand and analyze.
• Identifies slope and y-intercept: By converting to slope-intercept form, we can easily identify the slope and y-intercept of a line, which is essential for graphing and analysis.
• Enhances graphing: Slope-intercept form allows us to graph lines with precision, making it a valuable tool for visualizing and understanding linear relationships.
• Facilitates analysis: By converting linear equations to slope-intercept form, we can analyze and compare the slopes and y-intercepts of different lines, providing valuable insights into their behavior.

Converting to Slope-Intercept Form: A Step-by-Step Guide

Converting linear equations to slope-intercept form is a straightforward process that involves a few simple steps. Here's a step-by-step guide to help you master this technique:

Step 1: Write the Equation in Standard Form

The first step is to write the linear equation in standard form, which is Ax + By = C. This format allows us to easily identify the coefficients of x and y.

Example: 2x + 3y = 5

Step 2: Rearrange the Equation to Isolate y

Next, we need to rearrange the equation to isolate y. This involves moving the x term to the right-hand side of the equation and factoring out the coefficient of y.

Example: 3y = -2x + 5

Step 3: Divide Both Sides by the Coefficient of y

Now, we divide both sides of the equation by the coefficient of y (3) to solve for y.

Example: y = (-2/3)x + 5/3

Step 4: Write the Equation in Slope-Intercept Form

The final step is to write the equation in slope-intercept form, which is y = mx + b. In this case, the slope (m) is -2/3, and the y-intercept (b) is 5/3.

Example: y = (-2/3)x + 5/3

Practical Applications of Slope-Intercept Form

Slope-intercept form has numerous practical applications in various fields, including physics, engineering, economics, and computer science. Here are a few examples:

• Physics: Slope-intercept form is used to describe the motion of objects, including velocity and acceleration.
• Engineering: Slope-intercept form is used to design and analyze systems, including electrical circuits and mechanical systems.
• Economics: Slope-intercept form is used to model economic systems, including supply and demand curves.
• Computer Science: Slope-intercept form is used in computer graphics and game development to create realistic simulations.

Common Mistakes to Avoid

When converting linear equations to slope-intercept form, it's essential to avoid common mistakes that can lead to errors. Here are a few common mistakes to watch out for:

• Forgetting to divide both sides by the coefficient of y
• Misidentifying the slope and y-intercept
• Failing to rearrange the equation to isolate y

By following the step-by-step guide outlined above and avoiding common mistakes, you can master the art of converting linear equations to slope-intercept form.

Conclusion: Unlocking the Power of Slope-Intercept Form

Slope-intercept form is a powerful tool for analyzing and graphing linear equations. By mastering this technique, you can unlock the secrets of linear relationships and gain a deeper understanding of mathematical concepts. Whether you're a student, teacher, or math enthusiast, converting to slope-intercept form is an essential skill that will serve you well in your mathematical journey.

We hope this comprehensive guide has helped you understand the importance and benefits of slope-intercept form. With practice and patience, you can become proficient in converting linear equations to slope-intercept form and unlock the full potential of this powerful mathematical tool.

Now, it's your turn! Share your thoughts and experiences with slope-intercept form in the comments below. How do you use slope-intercept form in your math journey? What challenges have you faced, and how have you overcome them? Let's continue the conversation and explore the fascinating world of mathematics together!