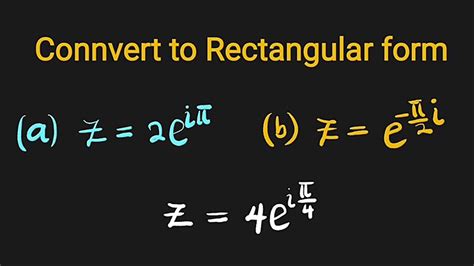Convert To Rectangular Form Made Easy

Quick Links :

Understanding Complex Numbers in Rectangular Form

Complex numbers are a crucial part of mathematics, particularly in algebra and calculus. They are used to represent quantities that have both magnitude and direction. However, working with complex numbers can be challenging, especially when they are expressed in polar form. Converting complex numbers to rectangular form can make them easier to work with. In this article, we will explore the concept of converting to rectangular form, its importance, and provide step-by-step instructions on how to do it.

Why Convert to Rectangular Form?

Converting complex numbers to rectangular form is essential in various mathematical operations, such as addition, subtraction, multiplication, and division. Rectangular form makes it easier to perform these operations, as it allows us to work with the real and imaginary parts of the complex number separately. Additionally, rectangular form is often required in applications such as electrical engineering, signal processing, and physics.

What is Rectangular Form?

Rectangular form is a way of expressing complex numbers in terms of their real and imaginary parts. A complex number in rectangular form is written as a + bi, where a is the real part and bi is the imaginary part. The real part represents the horizontal distance from the origin, while the imaginary part represents the vertical distance.

How to Convert to Rectangular Form

Converting a complex number from polar form to rectangular form involves using the trigonometric functions sine and cosine. The formula for converting a complex number from polar form to rectangular form is:

a + bi = r(cos(θ) + i sin(θ))

where r is the magnitude of the complex number, θ is the angle, and a and b are the real and imaginary parts, respectively.

Here are the steps to follow:

1. Identify the magnitude (r) and angle (θ) of the complex number in polar form.
2. Use the formula a = r cos(θ) to find the real part (a).
3. Use the formula b = r sin(θ) to find the imaginary part (b).
4. Write the complex number in rectangular form as a + bi.

Examples of Converting to Rectangular Form

Let's consider a few examples to illustrate the conversion process:

Example 1: Convert the complex number 3(cos(60°) + i sin(60°)) to rectangular form.

Using the formula, we get: a = 3 cos(60°) = 1.5 b = 3 sin(60°) = 2.6

The complex number in rectangular form is 1.5 + 2.6i.

Example 2: Convert the complex number 2(cos(45°) + i sin(45°)) to rectangular form.

Using the formula, we get: a = 2 cos(45°) = 1.4 b = 2 sin(45°) = 1.4

The complex number in rectangular form is 1.4 + 1.4i.

Common Mistakes to Avoid

When converting complex numbers to rectangular form, it's essential to avoid common mistakes that can lead to incorrect results. Here are some mistakes to watch out for:

• Incorrectly identifying the magnitude and angle of the complex number in polar form.
• Forgetting to use the trigonometric functions sine and cosine to find the real and imaginary parts.
• Writing the complex number in rectangular form with incorrect signs or coefficients.

Practical Applications of Rectangular Form

Rectangular form has numerous practical applications in various fields, including:

• Electrical engineering: Rectangular form is used to analyze and design electrical circuits, particularly in the context of AC circuits.
• Signal processing: Rectangular form is used to represent and manipulate signals in various signal processing applications.
• Physics: Rectangular form is used to describe the motion of objects in terms of their position, velocity, and acceleration.

Conclusion

Converting complex numbers to rectangular form is a crucial skill in mathematics, particularly in algebra and calculus. By understanding the concept of rectangular form and following the step-by-step instructions provided in this article, you can easily convert complex numbers to rectangular form. Remember to avoid common mistakes and apply the concept to practical problems in various fields.

We hope this article has helped you understand the concept of converting to rectangular form. If you have any questions or need further clarification, please feel free to comment below.