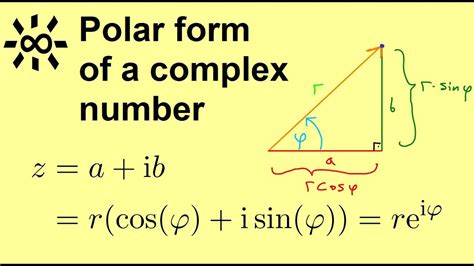Complex numbers have been a fundamental concept in mathematics and engineering for centuries. They have numerous applications in various fields, including signal processing, control systems, and electrical engineering. However, working with complex numbers can be challenging, especially when it comes to converting them into different forms. That's where a polar form calculator comes in handy.
Understanding Complex Numbers

Complex numbers are numbers that have both real and imaginary parts. They can be represented in the form a + bi, where 'a' is the real part and 'bi' is the imaginary part. The real part represents the x-coordinate, while the imaginary part represents the y-coordinate in the complex plane.
Importance of Complex Numbers
Complex numbers have numerous applications in various fields, including:
- Signal processing: Complex numbers are used to represent signals in the frequency domain.
- Control systems: Complex numbers are used to analyze and design control systems.
- Electrical engineering: Complex numbers are used to represent AC circuits and filter design.
What is Polar Form?

Polar form is a way of representing complex numbers in terms of their magnitude and angle. It is also known as trigonometric form. In polar form, a complex number is represented as r(cosθ + isinθ), where 'r' is the magnitude (or length) and 'θ' is the angle (or argument).
Benefits of Polar Form
Polar form has several benefits, including:
- Simplifies complex number arithmetic
- Provides a more intuitive understanding of complex numbers
- Facilitates the representation of complex numbers in graphical form
How to Convert Complex Numbers to Polar Form

Converting complex numbers to polar form involves the following steps:
- Calculate the magnitude (r) using the formula: r = √(a^2 + b^2)
- Calculate the angle (θ) using the formula: θ = arctan(b/a)
- Represent the complex number in polar form: r(cosθ + isinθ)
Polar Form Calculator
A polar form calculator is a tool that simplifies the process of converting complex numbers to polar form. It takes the real and imaginary parts of the complex number as input and provides the magnitude and angle as output.
Using a polar form calculator has several benefits, including:
- Saves time and effort
- Reduces errors
- Provides a more accurate representation of complex numbers
Applications of Polar Form Calculator

A polar form calculator has numerous applications in various fields, including:
- Signal processing: Polar form calculator can be used to represent signals in the frequency domain.
- Control systems: Polar form calculator can be used to analyze and design control systems.
- Electrical engineering: Polar form calculator can be used to represent AC circuits and filter design.
Conclusion
In conclusion, a polar form calculator is a powerful tool that simplifies the process of converting complex numbers to polar form. It has numerous applications in various fields and provides a more accurate representation of complex numbers. Whether you are a student, engineer, or researcher, a polar form calculator is an essential tool that can save you time and effort.
We hope this article has provided you with a comprehensive understanding of polar form calculator and its applications. If you have any questions or comments, please feel free to ask.
What is the difference between rectangular and polar form?
+Rectangular form represents complex numbers in terms of their real and imaginary parts, while polar form represents complex numbers in terms of their magnitude and angle.
How do I convert a complex number to polar form?
+To convert a complex number to polar form, calculate the magnitude (r) using the formula: r = √(a^2 + b^2) and calculate the angle (θ) using the formula: θ = arctan(b/a). Then, represent the complex number in polar form: r(cosθ + isinθ).
What are the benefits of using a polar form calculator?
+The benefits of using a polar form calculator include saving time and effort, reducing errors, and providing a more accurate representation of complex numbers.