3 Ways To Convert To Vertex Form Calculator

Quick Links :

Converting equations to vertex form can be a daunting task, especially when dealing with complex quadratic equations. Fortunately, with the help of a vertex form calculator, this process can be simplified and streamlined. In this article, we will explore three ways to convert equations to vertex form using a calculator, as well as provide a comprehensive understanding of the vertex form and its applications.

Understanding Vertex Form

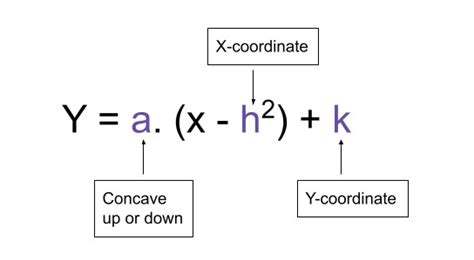
Vertex form is a way of expressing quadratic equations in the form y = a(x-h)^2 + k, where (h, k) represents the vertex of the parabola. This form is particularly useful when graphing quadratic equations, as it allows us to easily identify the vertex and axis of symmetry.

Benefits of Vertex Form

There are several benefits to using vertex form when working with quadratic equations. Some of the most significant advantages include:

• Easy identification of the vertex and axis of symmetry
• Simplified graphing and visualization
• Improved understanding of the equation's behavior and properties
• Enhanced problem-solving capabilities

Method 1: Using a Graphing Calculator

One way to convert an equation to vertex form using a calculator is by utilizing a graphing calculator. This method involves graphing the equation and using the calculator's built-in functions to identify the vertex and axis of symmetry.

To use this method, follow these steps:

1. Enter the equation into the graphing calculator.
2. Graph the equation using the calculator's built-in graphing function.
3. Use the calculator's "Maximum" or "Minimum" function to identify the vertex.
4. Record the coordinates of the vertex (h, k).
5. Rewrite the equation in vertex form using the values of h and k.

Example: Converting a Quadratic Equation to Vertex Form

Suppose we want to convert the equation y = x^2 + 4x + 3 to vertex form using a graphing calculator. Follow these steps:

1. Enter the equation into the graphing calculator.
2. Graph the equation using the calculator's built-in graphing function.
3. Use the calculator's "Minimum" function to identify the vertex.
4. Record the coordinates of the vertex (h, k) = (-2, -1).
5. Rewrite the equation in vertex form: y = (x+2)^2 - 1.

Method 2: Using a Vertex Form Calculator Online

Another way to convert an equation to vertex form is by using an online vertex form calculator. These calculators are specifically designed to convert quadratic equations to vertex form and can be a quick and efficient way to solve problems.

To use an online vertex form calculator, follow these steps:

1. Enter the equation into the online calculator.
2. Click the "Calculate" button to generate the vertex form.
3. Record the vertex form of the equation.

Example: Converting a Quadratic Equation to Vertex Form Online

Suppose we want to convert the equation y = x^2 + 4x + 3 to vertex form using an online calculator. Follow these steps:

1. Enter the equation into the online calculator.
2. Click the "Calculate" button to generate the vertex form.
3. Record the vertex form of the equation: y = (x+2)^2 - 1.

Method 3: Using a Scientific Calculator

A third way to convert an equation to vertex form is by using a scientific calculator. This method involves using the calculator's built-in algebraic functions to manipulate the equation and identify the vertex.

To use this method, follow these steps:

1. Enter the equation into the scientific calculator.
2. Use the calculator's algebraic functions to complete the square.
3. Identify the vertex (h, k) from the completed square.
4. Rewrite the equation in vertex form using the values of h and k.

Example: Converting a Quadratic Equation to Vertex Form Using a Scientific Calculator

Suppose we want to convert the equation y = x^2 + 4x + 3 to vertex form using a scientific calculator. Follow these steps:

1. Enter the equation into the scientific calculator.
2. Use the calculator's algebraic functions to complete the square: y = (x+2)^2 - 1.
3. Identify the vertex (h, k) = (-2, -1).
4. Rewrite the equation in vertex form: y = (x+2)^2 - 1.

Conclusion

Converting equations to vertex form can be a challenging task, but with the help of a vertex form calculator, this process can be simplified and streamlined. In this article, we explored three ways to convert equations to vertex form using a calculator, including using a graphing calculator, an online vertex form calculator, and a scientific calculator. By understanding the benefits and applications of vertex form, we can improve our problem-solving capabilities and gain a deeper understanding of quadratic equations.