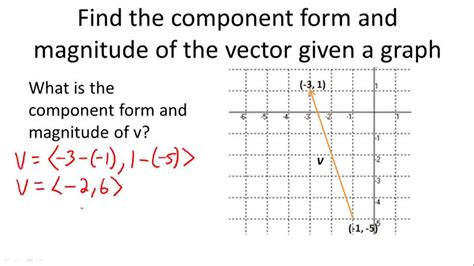
Understanding vectors is a fundamental aspect of mathematics and physics, and being able to express vectors in component form is a crucial skill for problem-solving in these fields. Vectors are quantities with both magnitude (amount of movement or force) and direction, and expressing them in component form allows us to analyze and manipulate them more easily.
What is Component Form of a Vector?

In essence, the component form of a vector is a way of representing a vector in terms of its horizontal and vertical components. This is particularly useful in two-dimensional spaces, where we can break down a vector into its x (horizontal) and y (vertical) components.
Why is Component Form Important?
Expressing vectors in component form is essential for various reasons:
- Simplifies calculations: Breaking down a vector into its components makes it easier to perform calculations, such as finding the magnitude and direction of the vector.
- Enhances problem-solving: Component form allows us to tackle complex problems by analyzing and manipulating the individual components of a vector.
- Facilitates visualization: By expressing a vector in component form, we can better visualize its direction and magnitude, making it easier to understand and work with.
How to Express a Vector in Component Form

To express a vector in component form, we need to follow these steps:
- Identify the vector: Start by identifying the vector you want to express in component form.
- Determine the horizontal and vertical components: Break down the vector into its horizontal (x) and vertical (y) components.
- Use the component form notation: Express the vector in component form using the notation (x, y), where x is the horizontal component and y is the vertical component.
Example: Finding the Component Form of a Vector
Suppose we have a vector A with a magnitude of 5 units and a direction of 30° above the x-axis. To express this vector in component form, we would follow these steps:
- Identify the vector: Vector A has a magnitude of 5 units and a direction of 30° above the x-axis.
- Determine the horizontal and vertical components: Using trigonometry, we can find the horizontal component (x) and vertical component (y) of the vector.
- Use the component form notation: Express the vector in component form using the notation (x, y).
By following these steps, we can find the component form of vector A as (4.33, 2.5).
Working with Component Form Vectors

Once we have expressed a vector in component form, we can perform various operations with it, such as:
- Adding and subtracting vectors: We can add and subtract vectors by adding and subtracting their corresponding components.
- Scaling vectors: We can scale a vector by multiplying its components by a scalar value.
- Finding the magnitude and direction: We can find the magnitude and direction of a vector using its components.
Example: Adding Vectors in Component Form
Suppose we have two vectors A (4, 2) and B (3, 1). To add these vectors, we would add their corresponding components:
- Horizontal component: 4 + 3 = 7
- Vertical component: 2 + 1 = 3
The resulting vector is (7, 3).
Real-World Applications of Component Form Vectors

Component form vectors have numerous real-world applications, including:
- Physics: Component form is used to describe the motion of objects in two-dimensional spaces, such as projectiles and circular motion.
- Engineering: Component form is used to analyze and design systems, such as bridges and buildings.
- Computer graphics: Component form is used to create 2D and 3D graphics, such as games and animations.
By understanding and working with component form vectors, we can tackle complex problems in various fields and create innovative solutions.
Conclusion: Mastering Component Form Vectors

In conclusion, expressing vectors in component form is a powerful tool for problem-solving and analysis. By mastering component form vectors, we can:
- Simplify complex calculations
- Enhance problem-solving skills
- Facilitate visualization and understanding
With practice and experience, working with component form vectors becomes second nature, allowing us to tackle challenging problems with confidence and accuracy.
Share your thoughts: What are some common challenges you face when working with vectors? How do you overcome these challenges? Share your experiences and tips in the comments below!
Take action: Practice working with component form vectors by trying out the examples and exercises provided. Experiment with different vectors and operations to become more comfortable with this powerful tool.
Get involved: Join online communities and forums to discuss vector-related topics and learn from others. Share your knowledge and expertise to help others master component form vectors.
Stay updated: Follow reputable sources and blogs to stay up-to-date with the latest developments and applications of component form vectors.
What is the purpose of expressing vectors in component form?
+Expressing vectors in component form simplifies calculations, enhances problem-solving, and facilitates visualization and understanding.
How do I add vectors in component form?
+To add vectors in component form, add their corresponding components. For example, if you have two vectors A (x1, y1) and B (x2, y2), the resulting vector is (x1 + x2, y1 + y2).
What are some real-world applications of component form vectors?
+Component form vectors have numerous real-world applications, including physics, engineering, and computer graphics.