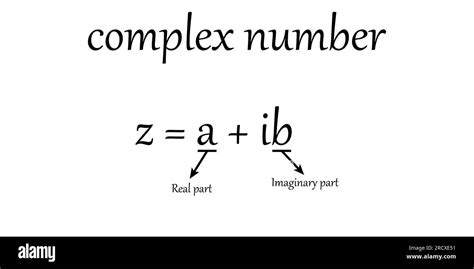Convert Complex Numbers To Standard Form In 3 Easy Steps

Quick Links :

Complex numbers are a fundamental concept in mathematics, particularly in algebra and calculus. They have numerous applications in physics, engineering, and computer science. However, working with complex numbers can be challenging, especially when it comes to converting them into standard form. In this article, we will break down the process into three easy steps, making it simpler for you to convert complex numbers to standard form.

Understanding Complex Numbers

A complex number is a number that can be expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit, satisfying the equation i^2 = -1. The real part of the complex number is 'a', and the imaginary part is 'bi'. For example, in the complex number 3 + 4i, 3 is the real part, and 4i is the imaginary part.

Why Convert Complex Numbers to Standard Form?

Converting complex numbers to standard form is essential in various mathematical operations, such as addition, subtraction, multiplication, and division. The standard form of a complex number is a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit. This form makes it easier to perform arithmetic operations and understand the properties of complex numbers.

Step 1: Simplify the Complex Number

The first step in converting a complex number to standard form is to simplify it. This involves combining like terms and eliminating any parentheses or brackets. For example, consider the complex number (2 + 3i) + (4 - 2i). To simplify this expression, we combine like terms: (2 + 4) + (3i - 2i) = 6 + i.

Example:

Simplify the complex number (3 + 2i) - (2 - i).

Solution: (3 - 2) + (2i + i) = 1 + 3i

Step 2: Write the Complex Number in a + bi Form

Once the complex number is simplified, the next step is to write it in a + bi form. This involves separating the real and imaginary parts of the complex number. For example, consider the complex number 2 + 3i. Here, '2' is the real part, and '3i' is the imaginary part.

Example:

Write the complex number 4 - 2i in a + bi form.

Solution: 4 - 2i is already in a + bi form, where '4' is the real part, and '-2i' is the imaginary part.

Step 3: Combine Like Terms (If Necessary)

In some cases, the complex number may have multiple like terms that need to be combined. This is the final step in converting the complex number to standard form. For example, consider the complex number 2 + 3i + 4 - i. To combine like terms, we add the real parts and the imaginary parts separately: (2 + 4) + (3i - i) = 6 + 2i.

Example:

Combine like terms in the complex number 3 + 2i + 2 - i.

Solution: (3 + 2) + (2i - i) = 5 + i

Conclusion and Final Thoughts

Converting complex numbers to standard form is a crucial skill in mathematics, and it can be achieved in three easy steps: simplify the complex number, write it in a + bi form, and combine like terms (if necessary). By mastering these steps, you can easily convert complex numbers to standard form and perform various mathematical operations with confidence.

We hope this article has been helpful in explaining the process of converting complex numbers to standard form. If you have any questions or need further clarification, please feel free to comment below. Share this article with your friends and classmates who may benefit from it.