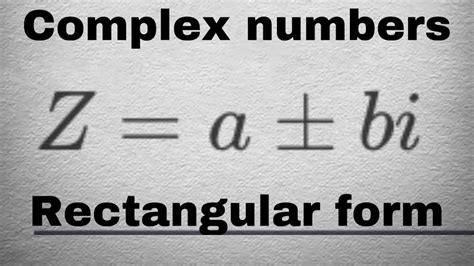The concept of complex numbers has been a cornerstone of mathematics and physics for centuries. One of the most important representations of complex numbers is the rectangular form, which provides a clear and concise way to express and manipulate complex numbers. In this article, we will delve into the world of complex numbers in rectangular form, exploring their definition, properties, and applications.
Complex numbers are an extension of the real number system, and they have the form a + bi, where a and b are real numbers, and i is the imaginary unit, defined as the square root of -1. The rectangular form of a complex number is a way of expressing it in terms of its real and imaginary parts.
What are Complex Numbers in Rectangular Form?

In rectangular form, a complex number is expressed as z = a + bi, where a is the real part, and b is the imaginary part. For example, the complex number 3 + 4i is in rectangular form, where 3 is the real part, and 4 is the imaginary part.
Properties of Complex Numbers in Rectangular Form
Complex numbers in rectangular form have several important properties that make them useful for a wide range of applications.
- Addition and Subtraction: Complex numbers can be added and subtracted by adding or subtracting their real and imaginary parts separately. For example, (a + bi) + (c + di) = (a + c) + (b + d)i.
- Multiplication: Complex numbers can be multiplied by multiplying their real and imaginary parts separately. For example, (a + bi)(c + di) = (ac - bd) + (ad + bc)i.
- Conjugation: The conjugate of a complex number is obtained by changing the sign of its imaginary part. For example, the conjugate of a + bi is a - bi.
Applications of Complex Numbers in Rectangular Form

Complex numbers in rectangular form have a wide range of applications in mathematics, physics, engineering, and computer science.
- Algebra: Complex numbers are used to solve equations that cannot be solved using real numbers alone.
- Calculus: Complex numbers are used to extend the concepts of calculus to complex-valued functions.
- Electrical Engineering: Complex numbers are used to analyze and design electrical circuits and filters.
- Computer Science: Complex numbers are used in computer graphics, game development, and scientific computing.
Working with Complex Numbers in Rectangular Form
Working with complex numbers in rectangular form involves performing arithmetic operations, such as addition, subtraction, multiplication, and division.
- Addition and Subtraction: To add or subtract complex numbers, simply add or subtract their real and imaginary parts separately.
- Multiplication: To multiply complex numbers, multiply their real and imaginary parts separately, and then combine the results.
- Division: To divide complex numbers, multiply the numerator and denominator by the conjugate of the denominator, and then simplify the result.
Examples of Complex Numbers in Rectangular Form

Here are a few examples of complex numbers in rectangular form:
- Example 1: Find the sum of 3 + 4i and 2 + 5i.
- Example 2: Find the product of 2 + 3i and 4 + 5i.
- Example 3: Find the quotient of 6 + 8i and 2 + 3i.
Solving Equations with Complex Numbers in Rectangular Form
Complex numbers in rectangular form can be used to solve equations that cannot be solved using real numbers alone.
- Linear Equations: Complex numbers can be used to solve linear equations of the form ax + bi = c + di.
- Quadratic Equations: Complex numbers can be used to solve quadratic equations of the form ax^2 + bx + c = 0.
Conclusion and Future Directions
In conclusion, complex numbers in rectangular form are a powerful tool for solving equations and performing arithmetic operations in a wide range of applications. By understanding the properties and applications of complex numbers in rectangular form, we can unlock new insights and solutions to complex problems.
We invite you to share your thoughts and questions about complex numbers in rectangular form. Have you worked with complex numbers in your studies or career? Share your experiences and insights in the comments below.