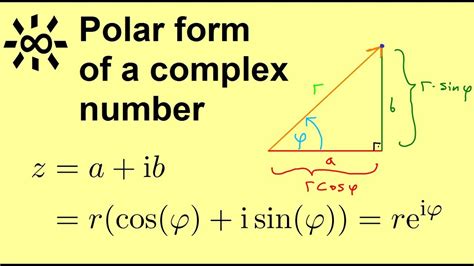The world of complex numbers can be quite daunting, but with the right tools and understanding, it can become a fascinating and manageable realm. One of the most powerful tools in the complex number toolkit is the polar form calculator, which can transform complex numbers into their polar equivalents. In this article, we will delve into the world of complex numbers, explore the concept of polar form, and discuss the inner workings of a complex number to polar form calculator.
What are Complex Numbers?

Complex numbers are an extension of the real number system, which includes all real numbers, as well as imaginary numbers. An imaginary number is a real number multiplied by the imaginary unit i, where i is the square root of -1. Complex numbers can be expressed in the form a + bi, where a is the real part and b is the imaginary part.
Real and Imaginary Parts
The real and imaginary parts of a complex number are crucial in understanding its behavior and properties. The real part of a complex number is the part that is not multiplied by i, while the imaginary part is the part that is multiplied by i.
Polar Form of a Complex Number

The polar form of a complex number is another way of expressing the same complex number, using the magnitude (length) and angle (direction) of the number. In polar form, a complex number can be written as r(cosθ + isinθ), where r is the magnitude and θ is the angle.
Magnitude and Angle
The magnitude of a complex number is its distance from the origin in the complex plane, while the angle is the direction from the positive real axis to the line connecting the origin to the complex number.
How to Convert Complex Numbers to Polar Form

Converting a complex number to polar form involves finding the magnitude and angle of the number. Here's a step-by-step process:
- Find the magnitude (r) using the formula r = √(a^2 + b^2), where a is the real part and b is the imaginary part.
- Find the angle (θ) using the formula θ = arctan(b/a), where a is the real part and b is the imaginary part.
- Express the complex number in polar form using the formula r(cosθ + isinθ).
Complex Number to Polar Form Calculator

A complex number to polar form calculator is a tool that can convert complex numbers to their polar equivalents. This calculator uses the formulas mentioned earlier to calculate the magnitude and angle of the complex number and then expresses the number in polar form.
Benefits of Using a Complex Number to Polar Form Calculator
Using a complex number to polar form calculator can be beneficial in various ways:
- It saves time and effort in converting complex numbers to polar form.
- It reduces the risk of errors in calculations.
- It provides a quick and easy way to visualize complex numbers in the polar form.
Common Applications of Polar Form Calculators

Polar form calculators have various applications in fields such as:
- Electrical engineering: Polar form is used to analyze and design AC circuits.
- Signal processing: Polar form is used to analyze and process signals in the frequency domain.
- Navigation: Polar form is used to calculate distances and angles in navigation systems.
Best Practices for Using a Polar Form Calculator
Here are some best practices for using a polar form calculator:
- Always check the calculator's accuracy and reliability.
- Understand the formulas and principles behind the calculator's calculations.
- Use the calculator as a tool to supplement your calculations, not replace them.
Conclusion
In conclusion, a complex number to polar form calculator is a powerful tool that can transform complex numbers into their polar equivalents. Understanding the concepts of complex numbers, polar form, and the inner workings of a polar form calculator can help you unlock the full potential of these calculators. Whether you're an engineer, scientist, or student, a polar form calculator can be a valuable addition to your toolkit.
Call to Action
If you're interested in learning more about complex numbers, polar form, or polar form calculators, we encourage you to explore our website for more resources and tutorials. Share your thoughts and questions in the comments below, and don't forget to like and share this article with your friends and colleagues.
What is the difference between rectangular and polar form of a complex number?
+The rectangular form of a complex number is a + bi, while the polar form is r(cosθ + isinθ). The rectangular form is more intuitive, while the polar form is more useful for calculations and visualizations.
How do I calculate the magnitude of a complex number?
+The magnitude of a complex number can be calculated using the formula r = √(a^2 + b^2), where a is the real part and b is the imaginary part.
Can I use a polar form calculator to convert rectangular coordinates to polar coordinates?
+Yes, a polar form calculator can be used to convert rectangular coordinates to polar coordinates. Simply enter the rectangular coordinates into the calculator, and it will output the polar coordinates.