Polar Form Of A Circle Explained Simply

Quick Links :

Polar Form of a Circle: Understanding the Basics

The polar form of a circle is a fundamental concept in mathematics, particularly in geometry and trigonometry. It provides a unique way of representing circles using polar coordinates, which is essential in various fields, including physics, engineering, and computer science. In this article, we will delve into the world of polar forms of circles, explaining the concept in simple terms, its benefits, and providing practical examples.

What is the Polar Form of a Circle?

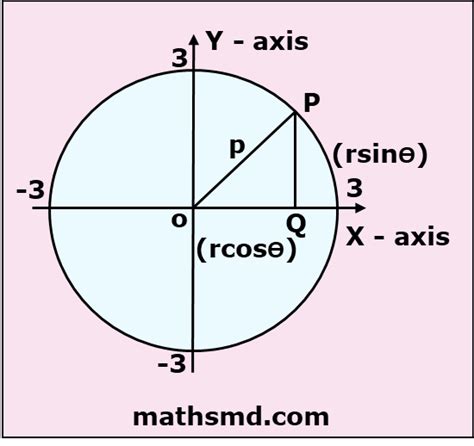
In the Cartesian coordinate system, a circle is represented as the set of all points equidistant from a fixed central point, called the center. The polar form of a circle extends this concept to the polar coordinate system, where a point is represented by its distance from the origin (radius) and the angle formed with the positive x-axis (azimuth).

The polar form of a circle is defined as the set of all points that satisfy the equation:

r = a

where 'r' is the radius, and 'a' is a constant. This equation represents a circle centered at the origin with a radius of 'a'.

Key Components of the Polar Form of a Circle

To understand the polar form of a circle, it's essential to grasp the following key components:

• Radius: The distance from the origin to any point on the circle.
• Azimuth: The angle formed by the radius with the positive x-axis.
• Center: The fixed point that is equidistant from all points on the circle.

Benefits of the Polar Form of a Circle

The polar form of a circle offers several benefits over the Cartesian representation:

• Simplifies complex calculations: The polar form simplifies calculations involving circles, especially when dealing with rotation, scaling, and translation.
• Provides a more intuitive representation: The polar form offers a more visual representation of circles, making it easier to understand and work with.
• Essential in various fields: The polar form is crucial in fields like physics, engineering, and computer science, where circular motion and geometry are prevalent.

Working with the Polar Form of a Circle

To work with the polar form of a circle, you need to understand the following steps:

1. Convert Cartesian coordinates to polar coordinates: To convert Cartesian coordinates (x, y) to polar coordinates (r, θ), use the following equations:

r = √(x^2 + y^2) θ = arctan(y/x)

2. Plot the circle: Using the polar coordinates, plot the circle on a polar coordinate system.
3. Perform calculations: Perform calculations involving the circle, such as finding the area, circumference, or equation of the circle.

Practical Examples

Let's consider a few practical examples to illustrate the polar form of a circle:

• Example 1: Find the polar form of a circle with a radius of 5 units and centered at the origin.

r = 5

• Example 2: Find the equation of a circle with a radius of 3 units and centered at the point (2, 3) in Cartesian coordinates.

First, convert the Cartesian coordinates to polar coordinates:

r = √(2^2 + 3^2) = √13 θ = arctan(3/2)

Then, write the equation of the circle in polar form:

r = √13

Conclusion and Call to Action

In conclusion, the polar form of a circle is a powerful tool for representing and working with circles in various fields. By understanding the basics, benefits, and steps involved in working with the polar form, you can unlock the full potential of this concept.

We encourage you to explore the world of polar coordinates and circles further. Share your thoughts, questions, or examples in the comments section below. Don't forget to share this article with your friends and colleagues who might find it helpful.