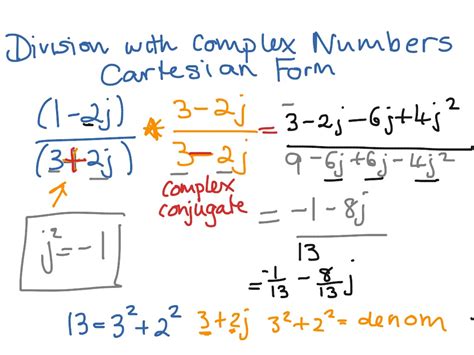Complex numbers have been a cornerstone of mathematics and engineering for centuries, allowing us to represent quantities that have both magnitude and direction. One of the most fundamental forms of representing complex numbers is the Cartesian form, also known as the rectangular form. In this article, we will delve into the world of complex numbers and explore the Cartesian form in depth.
What are Complex Numbers?

Complex numbers are numbers that have both real and imaginary parts. They are used to extend the real number system to the complex plane, allowing us to solve equations that cannot be solved using only real numbers. Complex numbers are denoted by the symbol C, and they have the form:
z = a + bi
where a is the real part and b is the imaginary part.
Real and Imaginary Parts
The real part of a complex number is the part that is not multiplied by the imaginary unit i. The imaginary part is the part that is multiplied by i. For example, in the complex number z = 3 + 4i, 3 is the real part and 4 is the imaginary part.
Cartesian Form of Complex Numbers

The Cartesian form of a complex number is a way of representing complex numbers in the form:
z = a + bi
where a is the real part and b is the imaginary part. This form is also known as the rectangular form because it represents complex numbers as points in the rectangular coordinate system.
Graphical Representation
Complex numbers can be represented graphically in the complex plane. The complex plane is a coordinate plane where the x-axis represents the real part and the y-axis represents the imaginary part. The point (a, b) in the complex plane represents the complex number z = a + bi.
Operations with Complex Numbers in Cartesian Form

Complex numbers in Cartesian form can be added, subtracted, multiplied, and divided using the following rules:
- Addition: (a + bi) + (c + di) = (a + c) + (b + d)i
- Subtraction: (a + bi) - (c + di) = (a - c) + (b - d)i
- Multiplication: (a + bi)(c + di) = (ac - bd) + (ad + bc)i
- Division: (a + bi)/(c + di) = ((ac + bd)/(c^2 + d^2)) + ((bc - ad)/(c^2 + d^2))i
Examples
- Add 3 + 4i and 2 + 5i: (3 + 4i) + (2 + 5i) = (3 + 2) + (4 + 5)i = 5 + 9i
- Subtract 3 + 4i from 2 + 5i: (2 + 5i) - (3 + 4i) = (2 - 3) + (5 - 4)i = -1 + i
- Multiply 3 + 4i and 2 + 5i: (3 + 4i)(2 + 5i) = (3(2) - 4(5)) + (3(5) + 4(2))i = -14 + 23i
- Divide 3 + 4i by 2 + 5i: (3 + 4i)/(2 + 5i) = ((3(2) + 4(5))/(2^2 + 5^2)) + ((4(2) - 3(5))/(2^2 + 5^2))i = (1/13) + (1/13)i
Applications of Cartesian Form of Complex Numbers

The Cartesian form of complex numbers has numerous applications in mathematics, physics, engineering, and other fields. Some of the applications include:
- Solving quadratic equations with complex roots
- Analyzing AC circuits in electrical engineering
- Representing sinusoidal signals in signal processing
- Performing calculations in geometry and trigonometry
Real-World Examples
- Electrical engineers use complex numbers to analyze AC circuits and design filters.
- Signal processing engineers use complex numbers to represent and manipulate sinusoidal signals.
- Physicists use complex numbers to describe the behavior of waves and oscillations.
Conclusion

In conclusion, the Cartesian form of complex numbers is a fundamental representation of complex numbers that has numerous applications in mathematics, physics, engineering, and other fields. By understanding the Cartesian form, we can perform calculations and solve problems that involve complex numbers.
What is the Cartesian form of complex numbers?
+The Cartesian form of complex numbers is a way of representing complex numbers in the form z = a + bi, where a is the real part and b is the imaginary part.
How do you add and subtract complex numbers in Cartesian form?
+To add complex numbers, add the real parts and add the imaginary parts. To subtract complex numbers, subtract the real parts and subtract the imaginary parts.
What are some applications of the Cartesian form of complex numbers?
+The Cartesian form of complex numbers has numerous applications in mathematics, physics, engineering, and other fields, including solving quadratic equations, analyzing AC circuits, and representing sinusoidal signals.
We hope this article has helped you understand the Cartesian form of complex numbers and its applications. If you have any questions or need further clarification, please leave a comment below. Share this article with your friends and colleagues who may be interested in learning about complex numbers.