Alternate Forms Of Derivatives Explained Simply

Quick Links :

Derivatives are a fundamental concept in calculus, and they have numerous applications in various fields, including physics, engineering, and economics. While the concept of derivatives is well-established, there are alternative forms of derivatives that can be used to solve problems in a more efficient and effective manner. In this article, we will explore these alternate forms of derivatives and explain them in simple terms.

What are Derivatives?

Before diving into alternate forms of derivatives, let's briefly review what derivatives are. A derivative measures how a function changes as its input changes. It represents the rate of change of the function with respect to one of its variables. In other words, it measures the slope of the tangent line to the function at a given point.

Limit Definition of a Derivative

The limit definition of a derivative is a fundamental concept in calculus. It states that the derivative of a function f(x) is defined as:

f'(x) = lim(h → 0) [f(x + h) - f(x)]/h

This definition provides a mathematical framework for calculating derivatives. However, it can be cumbersome to use in practice, especially for more complex functions.

Alternate Forms of Derivatives

Fortunately, there are alternate forms of derivatives that can simplify the calculation process. Some of these forms include:

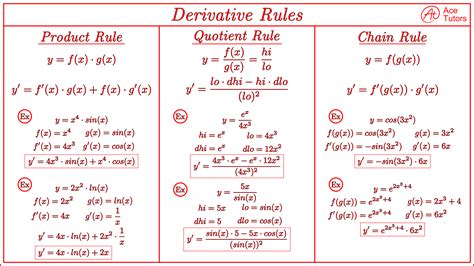
• Derivative Rules: Derivative rules provide a shortcut for calculating derivatives. For example, the power rule states that if f(x) = x^n, then f'(x) = nx^(n-1). There are many other derivative rules, including the product rule, quotient rule, and chain rule.
• Implicit Differentiation: Implicit differentiation is a technique used to find the derivative of an implicitly defined function. It involves differentiating both sides of the equation with respect to the independent variable.
• Logarithmic Differentiation: Logarithmic differentiation is a technique used to find the derivative of a function that involves logarithms. It involves taking the logarithm of both sides of the equation and then differentiating.

Derivative Rules Explained

Derivative rules are a set of formulas that provide a shortcut for calculating derivatives. Here are some of the most common derivative rules:

• Power Rule: If f(x) = x^n, then f'(x) = nx^(n-1)
• Product Rule: If f(x) = u(x)v(x), then f'(x) = u'(x)v(x) + u(x)v'(x)
• Quotient Rule: If f(x) = u(x)/v(x), then f'(x) = (u'(x)v(x) - u(x)v'(x))/v(x)^2
• Chain Rule: If f(x) = g(h(x)), then f'(x) = g'(h(x)) * h'(x)

These rules can be used to simplify the calculation of derivatives and make it easier to solve problems.

Implicit Differentiation Explained

Implicit differentiation is a technique used to find the derivative of an implicitly defined function. It involves differentiating both sides of the equation with respect to the independent variable.

For example, consider the equation:

x^2 + y^2 = 25

To find the derivative of y with respect to x, we can differentiate both sides of the equation with respect to x:

d/dx (x^2 + y^2) = d/dx (25)

Using the derivative rules, we get:

2x + 2y(dy/dx) = 0

Solving for dy/dx, we get:

dy/dx = -x/y

Logarithmic Differentiation Explained

Logarithmic differentiation is a technique used to find the derivative of a function that involves logarithms. It involves taking the logarithm of both sides of the equation and then differentiating.

For example, consider the equation:

y = log(x)

To find the derivative of y with respect to x, we can take the logarithm of both sides of the equation:

log(y) = log(log(x))

Using the derivative rules, we get:

dy/dx = 1/x

Conclusion

Alternate forms of derivatives, such as derivative rules, implicit differentiation, and logarithmic differentiation, can simplify the calculation of derivatives and make it easier to solve problems. These techniques provide a powerful tool for solving problems in calculus and have numerous applications in various fields.

We hope this article has provided a clear explanation of alternate forms of derivatives. If you have any questions or need further clarification, please don't hesitate to ask.