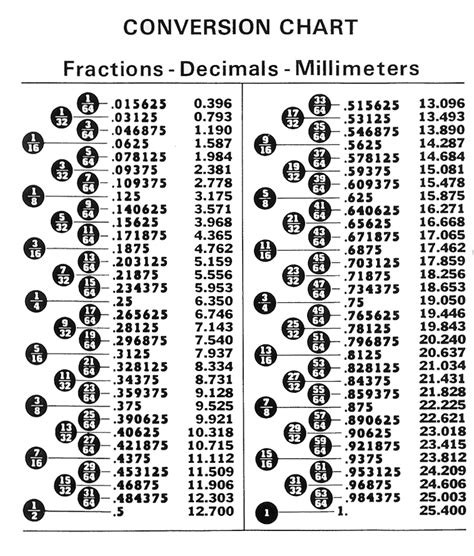
The concept of fractions and decimals is an essential part of mathematics, helping us understand and work with parts of a whole. Here, we're going to explore the conversion of the fraction 5 to 16 into its decimal form, explaining the process step by step and highlighting its significance in various aspects of mathematics and real-world applications.
Understanding Fractions and Decimals

Fractions and decimals are two ways to express the same value. A fraction represents a part of a whole as the ratio of two numbers, with the top number (numerator) telling us how many equal parts we have, and the bottom number (denominator) telling us how many parts the whole is divided into. Decimals, on the other hand, represent a value as a finite or infinite sequence of digits after a decimal point.
The Importance of Converting Fractions to Decimals
Converting fractions to decimals is a fundamental skill in mathematics and science, allowing for easier comparisons, additions, and subtractions of values. It is also crucial in practical applications, such as finance, engineering, and data analysis, where precise calculations are necessary.
The Process of Conversion

To convert the fraction 5 to 16 into a decimal, we divide the numerator (5) by the denominator (16).
Step-by-Step Conversion
- Understanding the Fraction: The fraction 5/16 means we have 5 equal parts out of a total of 16 parts.
- Dividing the Numerator by the Denominator: We perform the division 5 ÷ 16.
- Calculating the Decimal Form: By dividing 5 by 16, we get 0.3125.
Understanding the Decimal Form

The decimal form 0.3125 represents the same value as the fraction 5/16. It tells us that from the whole, we have a part that is equal to 3125/10000, or more simply, 31.25/100.
Practical Applications
- Finance: In finance, converting fractions to decimals is crucial for calculations involving interest rates, returns on investment, and more.
- Science and Engineering: Precise decimal values are essential in scientific and engineering applications for accurate calculations and analysis.
- Data Analysis: Decimal forms are easier to compare and analyze, making them preferred for statistical analysis and data interpretation.
Common Challenges and Solutions

- Challenge: Difficulty in converting complex fractions.
- Solution: Break down the fraction into simpler parts and convert each part separately.
Best Practices for Conversion
- Use a Calculator: For precise calculations, especially with complex fractions, use a calculator.
- Practice: Regular practice improves proficiency in converting fractions to decimals.
- Understand the Concept: Grasp the concept of fractions and decimals to easily convert between the two.
Conclusion and Future Directions

Mastering the conversion of fractions to decimals is a fundamental skill that opens doors to more complex mathematical operations and practical applications. By understanding and applying this conversion process, individuals can enhance their problem-solving skills and contribute to advancements in various fields.
We invite you to engage with this topic further by commenting below, sharing this article, or exploring more resources on fractions and decimals. How do you think the ability to convert fractions to decimals impacts your daily life or professional endeavors? Share your insights and start a conversation.
Why is converting fractions to decimals important?
+Converting fractions to decimals is important because it allows for easier comparisons and calculations in mathematics and science, and is crucial in practical applications such as finance, engineering, and data analysis.
How do you convert a fraction to a decimal?
+To convert a fraction to a decimal, you divide the numerator by the denominator. For example, the fraction 5/16 is converted to a decimal by dividing 5 by 16, resulting in 0.3125.
What are some practical applications of converting fractions to decimals?
+Practical applications include finance for calculations involving interest rates and returns on investment, science and engineering for precise calculations and analysis, and data analysis for statistical analysis and data interpretation.