Simplifying Fractions: What Is 36 In Simplest Form

Quick Links :

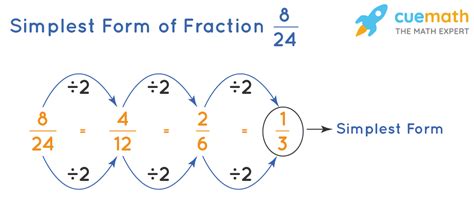
Reducing fractions to their simplest form is an essential concept in mathematics, making it easier to work with and understand numerical values. In this article, we will delve into the world of fractions, focusing on the concept of simplifying fractions and how to simplify the fraction 36.

Fractions are a way to represent part of a whole, and they are commonly used in various mathematical operations, such as addition, subtraction, multiplication, and division. However, working with complex fractions can be challenging, which is why simplifying fractions is crucial.

Why Simplify Fractions?

Simplifying fractions is essential for several reasons:

• It makes mathematical calculations easier and more manageable.
• It helps to avoid confusion and errors when working with fractions.
• It enables us to compare and order fractions more efficiently.
• It is a fundamental concept in mathematics, and understanding it is necessary for advanced mathematical concepts.

What Does it Mean to Simplify a Fraction?

Simplifying a fraction means reducing it to its simplest form by dividing both the numerator and denominator by the greatest common divisor (GCD). The GCD is the largest number that divides both numbers without leaving a remainder.

For example, consider the fraction 12/18. To simplify this fraction, we need to find the GCD of 12 and 18, which is 6. Dividing both numbers by 6 gives us 2/3, which is the simplified form of the fraction.

How to Simplify the Fraction 36

Now that we understand the concept of simplifying fractions, let's focus on the fraction 36. However, 36 is not a fraction; it is a whole number. Nevertheless, we can represent 36 as a fraction, such as 36/1.

To simplify the fraction 36/1, we need to find the GCD of 36 and 1, which is 1. Dividing both numbers by 1 gives us 36/1, which is already in its simplest form.

Simplifying Fractions with Different Numerators and Denominators

Let's consider a fraction with a different numerator and denominator, such as 36/48. To simplify this fraction, we need to find the GCD of 36 and 48, which is 12. Dividing both numbers by 12 gives us 3/4, which is the simplified form of the fraction.

Tips for Simplifying Fractions

Here are some tips to help you simplify fractions:

• Always find the greatest common divisor (GCD) of the numerator and denominator.
• Divide both numbers by the GCD to simplify the fraction.
• Make sure the simplified fraction is in its simplest form by checking if there are any common factors between the numerator and denominator.
• Practice simplifying fractions regularly to become more proficient.

Common Mistakes to Avoid When Simplifying Fractions

Here are some common mistakes to avoid when simplifying fractions:

• Not finding the greatest common divisor (GCD) of the numerator and denominator.
• Dividing both numbers by a number that is not the GCD.
• Not checking if the simplified fraction is in its simplest form.
• Not practicing simplifying fractions regularly.

Real-World Applications of Simplifying Fractions

Simplifying fractions has numerous real-world applications, including:

• Cooking and recipe measurement
• Music and rhythm
• Finance and budgeting
• Science and engineering
• Art and design

Conclusion

Simplifying fractions is a fundamental concept in mathematics that makes mathematical calculations easier and more manageable. By understanding the concept of simplifying fractions and practicing regularly, you can become more proficient in mathematics and apply it to various real-world applications. Remember to always find the greatest common divisor (GCD) of the numerator and denominator and divide both numbers by the GCD to simplify the fraction.