3 In Decimal Form Made Easy

Quick Links :

The decimal system is a fundamental concept in mathematics that has been a cornerstone of numerical representation for centuries. Understanding and working with decimals can be a challenging task for many students and individuals. However, with the right approach and techniques, decimals can be made easy to comprehend and manipulate.

Decimals are a way of expressing fractions in a more compact and readable form. They are used to represent numbers that have a fractional part, such as 3.14 or 0.5. The decimal system is based on the concept of place value, where each digit in a number has a specific value depending on its position.

Understanding Decimal Places

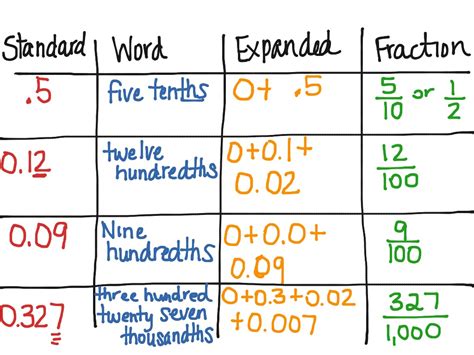
One of the key concepts in working with decimals is understanding the different decimal places. The decimal places are the digits that appear after the decimal point. Each decimal place has a specific value, with the first place representing tenths, the second place representing hundredths, and so on.

For example, the number 3.14 has two decimal places. The first place represents tenths, and the second place represents hundredths. Therefore, the number 3.14 can be read as "three and fourteen hundredths."

Reading and Writing Decimals

Reading and writing decimals can be a bit tricky, but with practice, it becomes easier. When reading decimals, it's essential to pay attention to the decimal places and the value they represent.

For example, the number 0.5 can be read as "five tenths" or "one half." The number 2.75 can be read as "two and seventy-five hundredths."

When writing decimals, it's essential to use the correct notation. The decimal point is used to separate the whole number part from the fractional part.

Adding and Subtracting Decimals

Adding and subtracting decimals is similar to adding and subtracting whole numbers. However, it's essential to line up the decimal points and add or subtract the corresponding decimal places.

For example, to add 2.5 and 1.8, line up the decimal points and add the corresponding decimal places.

2.5 +1.8

4.3

When subtracting decimals, it's essential to line up the decimal points and subtract the corresponding decimal places.

For example, to subtract 1.2 from 3.5, line up the decimal points and subtract the corresponding decimal places.

3.5 -1.2

2.3

Multiplying Decimals

Multiplying decimals is similar to multiplying whole numbers. However, it's essential to multiply the decimal places and then add the corresponding decimal places.

For example, to multiply 2.5 and 1.8, multiply the whole number part and then multiply the decimal places.

2.5 x 1.8 = 4.5

When multiplying decimals, it's essential to multiply the corresponding decimal places and then add the results.

Dividing Decimals

Dividing decimals is similar to dividing whole numbers. However, it's essential to divide the decimal places and then add the corresponding decimal places.

For example, to divide 4.5 by 1.5, divide the whole number part and then divide the decimal places.

4.5 ÷ 1.5 = 3

When dividing decimals, it's essential to divide the corresponding decimal places and then add the results.

Real-World Applications of Decimals

Decimals have many real-world applications, from finance to science. Understanding decimals is essential for calculating percentages, interest rates, and other financial metrics.

In science, decimals are used to represent measurements and calculate quantities. For example, the circumference of a circle is calculated using the formula C = 2πr, where C is the circumference, π is the mathematical constant pi, and r is the radius.

Decimals are also used in engineering to represent measurements and calculate quantities. For example, the length of a bridge is calculated using the formula L = πr^2, where L is the length, π is the mathematical constant pi, and r is the radius.

Common Mistakes When Working with Decimals

When working with decimals, it's common to make mistakes. Here are some common mistakes to avoid:

• Not lining up the decimal points when adding or subtracting decimals
• Not multiplying the corresponding decimal places when multiplying decimals
• Not dividing the corresponding decimal places when dividing decimals
• Not using the correct notation when writing decimals

By avoiding these common mistakes, you can ensure that you work with decimals accurately and efficiently.

Tips for Mastering Decimals

Here are some tips for mastering decimals:

• Practice, practice, practice: The more you practice working with decimals, the more comfortable you will become.
• Use real-world examples: Use real-world examples to illustrate the application of decimals.
• Use visual aids: Use visual aids such as charts and graphs to illustrate the concept of decimals.
• Break it down: Break down complex decimal problems into simpler components.

By following these tips, you can master decimals and improve your math skills.

Conclusion

In conclusion, decimals are an essential concept in mathematics that can be made easy to comprehend and manipulate with the right approach and techniques. By understanding decimal places, reading and writing decimals, adding and subtracting decimals, multiplying and dividing decimals, and avoiding common mistakes, you can master decimals and improve your math skills.

We hope this article has been informative and helpful. Please share your thoughts and comments below.