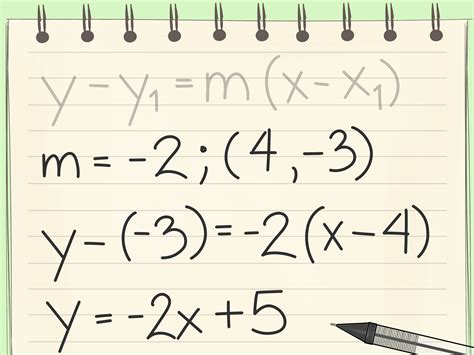3 Ways To Master Slope Intercept Form

Quick Links :

Mastering the slope-intercept form is a crucial skill for any student of mathematics, particularly those who are looking to excel in algebra and beyond. The slope-intercept form, often denoted as y = mx + b, is a fundamental concept in understanding linear equations and their graphical representations. In this article, we will delve into three effective ways to master the slope-intercept form, providing you with a comprehensive understanding of this essential mathematical concept.

Understanding the Basics of Slope-Intercept Form

To start, it's essential to understand the components of the slope-intercept form. The equation y = mx + b consists of three critical elements:

• m: The slope of the line, which represents the rate of change between the x and y variables.
• b: The y-intercept, which is the point at which the line intersects the y-axis.
• x and y: The variables that represent the coordinates of any point on the line.

Visualizing the Slope-Intercept Form

Visualizing the slope-intercept form can be incredibly helpful in understanding its components. By plotting the y-intercept (b) on the y-axis and then using the slope (m) to determine the rise and run of the line, you can effectively graph linear equations.

For example, consider the equation y = 2x + 3. In this case, the y-intercept (b) is 3, so the line intersects the y-axis at the point (0, 3). The slope (m) is 2, which means that for every one unit increase in x, the line rises two units.

Way 1: Practice, Practice, Practice

One of the most effective ways to master the slope-intercept form is through practice. The more you work with linear equations in slope-intercept form, the more comfortable you'll become with identifying the slope and y-intercept.

Here are a few practice exercises to get you started:

• Convert the following linear equations to slope-intercept form:
  • 2x + 3y = 5
  • x - 2y = -3
  • 4x - 5y = 2
• Graph the following linear equations:
  • y = 2x - 1
  • y = -3x + 2
  • y = x + 1

Using Online Resources to Practice

There are numerous online resources available to help you practice working with the slope-intercept form. Some popular options include:

• Khan Academy: Khan Academy offers a wide range of practice exercises and video tutorials on linear equations and slope-intercept form.
• Mathway: Mathway is an online math problem solver that can help you work through practice exercises and check your answers.
• IXL: IXL is an online learning platform that offers practice exercises and games for a variety of math topics, including linear equations and slope-intercept form.

Way 2: Use Real-World Applications

Using real-world applications is an excellent way to make the slope-intercept form more meaningful and interesting. By relating linear equations to real-life scenarios, you can better understand the practical significance of the slope and y-intercept.

Here are a few examples of real-world applications of the slope-intercept form:

• Cost-Benefit Analysis: The slope-intercept form can be used to model the relationship between the cost of producing a product and the number of units sold.
• Physics: The slope-intercept form can be used to describe the motion of an object, where the slope represents the velocity and the y-intercept represents the initial position.
• Finance: The slope-intercept form can be used to model the relationship between the interest rate on a loan and the amount borrowed.

Creating Your Own Real-World Applications

Try creating your own real-world applications of the slope-intercept form. For example:

• Research the cost of producing a product and create a linear equation to model the relationship between the cost and the number of units sold.
• Investigate the motion of an object and create a linear equation to describe its velocity and initial position.
• Look into the interest rates on loans and create a linear equation to model the relationship between the interest rate and the amount borrowed.

Way 3: Use Visual Aids and Graphing Tools

Using visual aids and graphing tools can be incredibly helpful in mastering the slope-intercept form. By visualizing linear equations and graphing their slopes and y-intercepts, you can gain a deeper understanding of the relationships between variables.

Here are a few visual aids and graphing tools you can use:

• Graph paper: Graph paper is a simple yet effective tool for graphing linear equations. By plotting the x and y intercepts and using the slope to determine the rise and run, you can visualize the line and its components.
• Graphing calculators: Graphing calculators are powerful tools that can help you graph linear equations and explore their properties.
• Online graphing tools: There are numerous online graphing tools available, including GeoGebra and Desmos, that can help you visualize linear equations and explore their properties.

Exploring the Benefits of Visual Aids and Graphing Tools

Using visual aids and graphing tools can have numerous benefits, including:

• Improved understanding: Visualizing linear equations can help you gain a deeper understanding of the relationships between variables.
• Increased accuracy: Graphing tools can help you accurately graph linear equations and identify their components.
• Enhanced problem-solving skills: By exploring the properties of linear equations using visual aids and graphing tools, you can develop your problem-solving skills and become more proficient in working with the slope-intercept form.

In conclusion, mastering the slope-intercept form requires practice, patience, and persistence. By using real-world applications, visual aids, and graphing tools, you can gain a deeper understanding of this essential mathematical concept and become more proficient in working with linear equations.

If you have any questions or comments, please feel free to share them below. We'd love to hear from you!