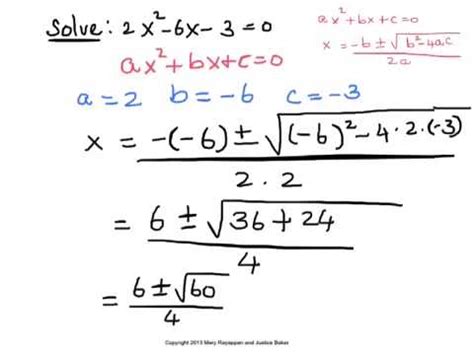Simplify Equations With The 21 Simplest Form

Quick Links :

Simplifying Equations: A Guide to Reducing Complexity

Equations are a fundamental part of mathematics, and simplifying them is an essential skill for anyone looking to grasp mathematical concepts. Simplifying equations involves breaking down complex expressions into simpler forms, making it easier to solve and understand the underlying relationships. In this article, we'll explore the simplest form of equations and provide a comprehensive guide on how to simplify them.

Why Simplify Equations?

Simplifying equations is crucial in mathematics as it:

• Makes equations easier to solve and understand
• Reduces the complexity of mathematical expressions
• Helps identify patterns and relationships between variables
• Enhances problem-solving skills and critical thinking

Types of Equations

Before diving into simplification techniques, it's essential to understand the different types of equations:

• Linear equations: Equations in which the highest power of the variable(s) is 1.
• Quadratic equations: Equations in which the highest power of the variable(s) is 2.
• Polynomial equations: Equations in which the highest power of the variable(s) is more than 2.

21 Simplest Form of Equations

Here are 21 simple equations in their simplest form, covering various types of equations:

1. 2x = 6
2. x + 3 = 7
3. x - 2 = 5
4. x/4 = 9
5. 2x + 5 = 11
6. x^2 + 4x + 4 = 0
7. x^2 - 9 = 0
8. x^3 - 27 = 0
9. 2x^2 + 5x - 3 = 0
10. x^2 - 4x - 3 = 0
11. x^2 + 2x - 15 = 0
12. 2x^2 - 7x - 4 = 0
13. x^2 - 3x - 10 = 0
14. x^2 + 5x + 6 = 0
15. 2x^2 + 3x - 2 = 0
16. x^2 - 2x - 6 = 0
17. x^2 + x - 12 = 0
18. 2x^2 - 5x - 3 = 0
19. x^2 + 4x - 5 = 0
20. x^2 - x - 6 = 0
21. 2x^2 + x - 3 = 0

Simplification Techniques

Now that we've explored the simplest form of equations, let's dive into the techniques used to simplify complex equations:

• Combine like terms: Combine terms with the same variable and coefficient.
• Eliminate parentheses: Distribute the terms inside the parentheses to simplify the equation.
• Use inverse operations: Apply inverse operations to isolate variables and simplify the equation.

Step-by-Step Simplification Process

Here's a step-by-step guide to simplify complex equations:

1. Read and understand the equation
2. Identify the variables and coefficients
3. Combine like terms
4. Eliminate parentheses
5. Use inverse operations to isolate variables
6. Check for consistency and accuracy

Common Mistakes to Avoid

When simplifying equations, it's essential to avoid common mistakes:

• Incorrectly combining like terms
• Failing to eliminate parentheses
• Misapplying inverse operations
• Not checking for consistency and accuracy

Real-World Applications

Simplifying equations has numerous real-world applications:

• Physics and engineering: Simplifying equations is crucial in understanding complex systems and relationships.
• Computer science: Simplifying equations is used in algorithms and data analysis.
• Economics: Simplifying equations is used in modeling economic systems and predicting trends.

Conclusion

Simplifying equations is a fundamental skill in mathematics, and understanding the simplest form of equations is crucial in developing problem-solving skills. By mastering simplification techniques and avoiding common mistakes, individuals can effectively simplify complex equations and apply mathematical concepts to real-world problems.

Now that you've learned the basics of simplifying equations, we encourage you to practice and apply these skills to real-world problems. Share your experiences and insights in the comments below!