Mastering Slope Intercept Form: 2-1 Additional Practice

Quick Links :

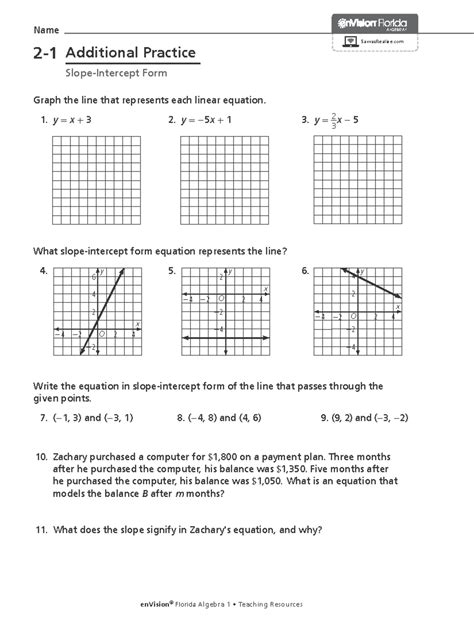
In the world of mathematics, algebra is a fundamental subject that helps us solve problems and understand various phenomena. One of the essential concepts in algebra is the slope-intercept form, which is widely used in graphing linear equations. In this article, we will delve into the world of slope-intercept form and provide additional practice to help you master this concept.

Understanding Slope Intercept Form

The slope-intercept form is a way of expressing a linear equation in the form y = mx + b, where m represents the slope of the line, and b represents the y-intercept. The slope-intercept form is useful for graphing linear equations and understanding the relationship between the variables.

Key Components of Slope Intercept Form

• Slope (m): The slope represents the rate of change of the line. It can be positive, negative, or zero.
• Y-intercept (b): The y-intercept represents the point at which the line intersects the y-axis.

How to Graph a Linear Equation in Slope Intercept Form

Graphing a linear equation in slope-intercept form involves two steps: finding the y-intercept and using the slope to plot additional points.

1. Find the Y-intercept: To find the y-intercept, substitute x = 0 into the equation and solve for y. This will give you the point at which the line intersects the y-axis.
2. Use the Slope to Plot Additional Points: Once you have the y-intercept, use the slope to plot additional points on the line. The slope represents the rate of change, so for every unit increase in x, the y-value will increase or decrease by the slope.

Examples and Practice

Here are a few examples to help you practice graphing linear equations in slope-intercept form:

• Example 1: Graph the equation y = 2x + 1
  • Find the y-intercept by substituting x = 0 into the equation: y = 2(0) + 1 = 1
  • Use the slope to plot additional points: for every unit increase in x, the y-value will increase by 2
• Example 2: Graph the equation y = -3x - 2
  • Find the y-intercept by substituting x = 0 into the equation: y = -3(0) - 2 = -2
  • Use the slope to plot additional points: for every unit increase in x, the y-value will decrease by 3

Practice Exercises

Practice makes perfect! Here are some additional practice exercises to help you master the slope-intercept form:

• Exercise 1: Graph the equation y = x - 2
• Exercise 2: Graph the equation y = -2x + 3
• Exercise 3: Graph the equation y = 4x - 1

Common Applications of Slope Intercept Form

The slope-intercept form has numerous applications in real-life scenarios, including:

• Physics and Engineering: The slope-intercept form is used to model the motion of objects and understand the relationship between variables.
• Economics: The slope-intercept form is used to model the relationship between economic variables, such as supply and demand.
• Computer Science: The slope-intercept form is used in programming and algorithm design to solve problems and optimize solutions.

Conclusion

Mastering the slope-intercept form is an essential skill in algebra, and with practice, you can become proficient in graphing linear equations and understanding the relationship between variables. Remember to practice regularly and apply the concepts to real-life scenarios to reinforce your understanding.

Take the Next Step

Now that you have a solid understanding of the slope-intercept form, take the next step by practicing the exercises and exploring real-life applications. Share your experiences and ask questions in the comments below. Don't forget to share this article with your friends and classmates to help them master the slope-intercept form.