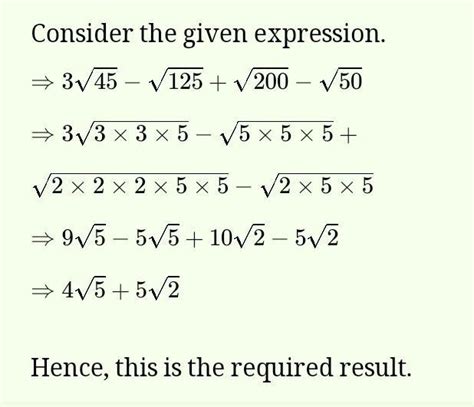The concept of simplifying radicals can seem daunting, but it's actually a straightforward process that can be broken down into simple steps. In this article, we'll explore how to simplify √125 in 5 easy steps.
Simplifying radicals is an essential math skill that can help you solve equations, manipulate algebraic expressions, and even tackle complex calculus problems. But before we dive into the steps, let's take a moment to understand why simplifying radicals is important.
Why Simplify Radicals?

Radicals, or roots, are used to represent the nth root of a number. However, when working with radicals, it's often necessary to simplify them to make calculations easier. Simplifying radicals helps to:
- Reduce complexity: Simplifying radicals makes it easier to work with equations and expressions.
- Improve readability: Simplified radicals are easier to read and understand.
- Enhance calculations: Simplified radicals make calculations faster and more accurate.
Now that we've established the importance of simplifying radicals, let's move on to the 5 easy steps to simplify √125.
Step 1: Identify the Radical

The first step is to identify the radical that needs to be simplified. In this case, we're working with √125.
What is a Radical?
A radical, or root, is a mathematical expression that represents the nth root of a number. The most common radical is the square root (√), which represents the second root of a number.
Step 2: Find the Factors of 125

To simplify √125, we need to find the factors of 125. Factors are the numbers that divide a given number without leaving a remainder.
- 125 = 1 × 125
- 125 = 5 × 25
Prime Factorization
We can further simplify the factors by finding the prime factorization of 125. Prime factorization is the process of breaking down a number into its prime factors.
- 125 = 5 × 5 × 5 (or 5^3)
Step 3: Identify the Perfect Square

Now that we have the prime factorization of 125, we can identify the perfect square.
- 125 = 5^3
- 5^2 = 25 (perfect square)
What is a Perfect Square?
A perfect square is a number that can be expressed as the square of an integer. In this case, 25 is a perfect square because it can be expressed as 5^2.
Step 4: Simplify the Radical

Now that we've identified the perfect square, we can simplify the radical.
- √125 = √(5^2 × 5)
- √125 = 5√5
Simplifying Radicals with Variables
When simplifying radicals with variables, it's essential to factor out any perfect squares from the radicand.
Step 5: Verify the Simplification

The final step is to verify the simplification by plugging the simplified radical back into the original equation.
- √125 = 5√5
- (√125)^2 = (5√5)^2
- 125 = 25 × 5
- 125 = 125
By following these 5 easy steps, we've successfully simplified √125 to 5√5.
What is the purpose of simplifying radicals?
+The purpose of simplifying radicals is to reduce complexity, improve readability, and enhance calculations.
How do I find the prime factorization of a number?
+Prime factorization is the process of breaking down a number into its prime factors. You can find the prime factorization by dividing the number by its smallest prime factor, then dividing the result by the next smallest prime factor, and so on.
What is a perfect square?
+A perfect square is a number that can be expressed as the square of an integer. For example, 25 is a perfect square because it can be expressed as 5^2.
We hope this article has helped you understand the process of simplifying radicals. Remember to practice simplifying radicals with different numbers and variables to become more comfortable with the process. Share your thoughts and questions in the comments below, and don't forget to share this article with your friends and classmates!