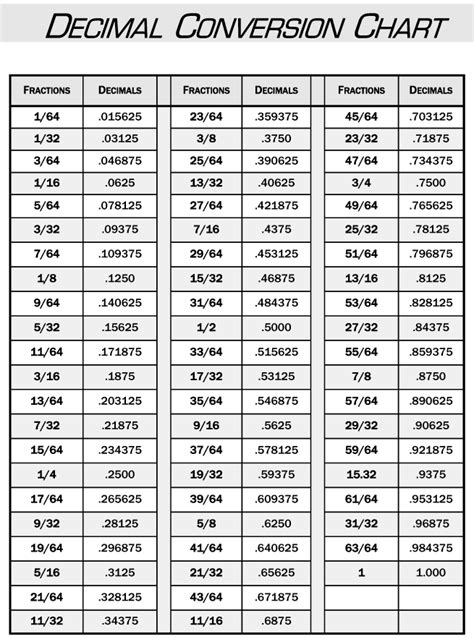
The number 12 is a decimal number that can be easily converted to other number systems, such as binary, hexadecimal, and octal. In this article, we will focus on the decimal form of 12, exploring its significance, uses, and conversion methods.
The Importance of Decimal Numbers
Decimal numbers are the most commonly used number system in everyday life. They are used to represent quantities, measurements, and calculations in various fields, including science, technology, engineering, and mathematics (STEM). Decimal numbers are also used in finance, commerce, and education. The decimal system is based on 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Understanding Decimal Numbers
Decimal numbers are made up of digits that are arranged in a specific pattern. The rightmost digit is called the units place, followed by the tens place, hundreds place, and so on. Each digit in a decimal number has a place value that is determined by its position. For example, in the number 12, the digit 1 is in the tens place, and the digit 2 is in the units place.

Converting 12 to Other Number Systems
While 12 is a decimal number, it can be converted to other number systems, such as binary, hexadecimal, and octal. These conversions are useful in computer programming, data storage, and digital electronics.
Binary Conversion
Binary numbers are made up of two digits: 0 and 1. To convert 12 to binary, we need to find the binary equivalent of each digit.

The binary equivalent of 12 is 1100.
Hexadecimal Conversion
Hexadecimal numbers are made up of 16 digits: 0-9 and A-F. To convert 12 to hexadecimal, we need to find the hexadecimal equivalent of each digit.

The hexadecimal equivalent of 12 is C.
Octal Conversion
Octal numbers are made up of eight digits: 0-7. To convert 12 to octal, we need to find the octal equivalent of each digit.

The octal equivalent of 12 is 14.
Practical Applications of Decimal Numbers
Decimal numbers have numerous practical applications in various fields, including:
- Finance: Decimal numbers are used to represent monetary values, interest rates, and investment returns.
- Science: Decimal numbers are used to represent scientific measurements, such as temperature, pressure, and velocity.
- Engineering: Decimal numbers are used to represent engineering measurements, such as length, width, and height.
- Education: Decimal numbers are used to represent educational measurements, such as grades, scores, and percentages.
Conclusion
In conclusion, 12 is a decimal number that can be easily converted to other number systems, such as binary, hexadecimal, and octal. Understanding decimal numbers and their conversions is essential in various fields, including finance, science, engineering, and education. By mastering decimal numbers, we can perform calculations, measurements, and conversions with ease and accuracy.
What's Next?
Now that you have learned about the decimal form of 12, you can explore other number systems and conversions. You can practice converting decimal numbers to binary, hexadecimal, and octal, and apply your knowledge to real-world problems. Remember to share your thoughts and questions in the comments section below.
FAQs
What is the binary equivalent of 12?
+The binary equivalent of 12 is 1100.
What is the hexadecimal equivalent of 12?
+The hexadecimal equivalent of 12 is C.
What is the octal equivalent of 12?
+The octal equivalent of 12 is 14.