Simplifying fractions is a fundamental concept in mathematics that can seem daunting at first, but with practice and patience, it can become second nature. In this article, we will delve into the world of simplifying fractions, exploring the concepts, rules, and examples to help you master this essential math skill.
What is a Fraction?

A fraction is a way to represent a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator tells us how many equal parts we have, while the denominator tells us how many parts the whole is divided into.
Why Simplify Fractions?

Simplifying fractions is essential in mathematics because it helps us to:
- Reduce clutter and make calculations easier
- Compare fractions more easily
- Add and subtract fractions more efficiently
- Solve equations and problems more effectively
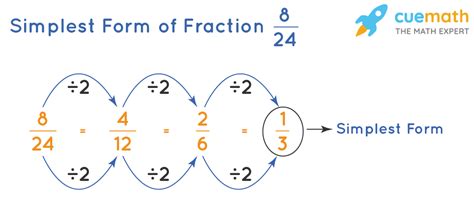
How to Simplify Fractions

To simplify a fraction, follow these steps:
- Find the greatest common divisor (GCD): The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
- Divide both numbers by the GCD: Divide the numerator and denominator by the GCD to simplify the fraction.
Example 1: Simplifying a Simple Fraction

Simplify the fraction: 6/8
- Find the GCD: 2
- Divide both numbers by the GCD: 6 ÷ 2 = 3, 8 ÷ 2 = 4
- Simplified fraction: 3/4
Rules for Simplifying Fractions

Here are some essential rules to keep in mind when simplifying fractions:
- Simplify before adding or subtracting: Always simplify fractions before adding or subtracting them.
- Cancel out common factors: Cancel out any common factors between the numerator and denominator.
- Reduce to lowest terms: Reduce the fraction to its lowest terms by dividing both numbers by their GCD.
Example 2: Simplifying a Complex Fraction

Simplify the fraction: 12/16
- Find the GCD: 4
- Divide both numbers by the GCD: 12 ÷ 4 = 3, 16 ÷ 4 = 4
- Simplified fraction: 3/4
Common Mistakes to Avoid

Here are some common mistakes to avoid when simplifying fractions:
- Not finding the GCD: Make sure to find the GCD before simplifying the fraction.
- Not canceling out common factors: Cancel out any common factors between the numerator and denominator.
- Not reducing to lowest terms: Reduce the fraction to its lowest terms by dividing both numbers by their GCD.
Practical Applications of Simplifying Fractions

Simplifying fractions has numerous practical applications in:
- Cooking and recipes: Simplifying fractions helps with scaling recipes and measuring ingredients.
- Finance and economics: Simplifying fractions is essential for calculating interest rates, investment returns, and budgeting.
- Science and engineering: Simplifying fractions is crucial for calculating quantities, measuring rates, and understanding scientific concepts.
Conclusion
Simplifying fractions is a fundamental math skill that requires practice and patience. By following the steps and rules outlined in this article, you can master the art of simplifying fractions and improve your math skills. Remember to always simplify fractions before adding or subtracting, cancel out common factors, and reduce to lowest terms.We hope this article has helped you understand the importance of simplifying fractions and how to do it effectively. If you have any questions or comments, please feel free to share them below.
What is the purpose of simplifying fractions?
+Simplifying fractions helps to reduce clutter, make calculations easier, compare fractions more easily, add and subtract fractions more efficiently, and solve equations and problems more effectively.
How do I simplify a fraction?
+To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator, and then divide both numbers by the GCD.
What are some common mistakes to avoid when simplifying fractions?
+Common mistakes to avoid include not finding the GCD, not canceling out common factors, and not reducing to lowest terms.